题目内容
19.等差数列{an}中,a1<0,S8=S13,使得前n项和Sn取到最小值的n的值为10或11.分析 设等差数列的公差为d,根据等差数列的前n项和的公式化简S8=S13,得到首项与公差的关系式,结合一元二次函数的性质进行求解即可.
解答 解:由S8=S13得:
8a1+$\frac{8×7}{2}$d=13a1+$\frac{13×12}{2}$d,
解得:a1=-10d,又a1<0,得到d>0,
所以Sn=na1+$\frac{n×(n-1)}{2}$d=$\frac{d}{2}$n2+(a1-$\frac{d}{2}$)n,
由d>0,得到Sn是一个关于n的开口向上抛物线,且S8=S13,
则函数的对称轴为n=$\frac{8+13}{2}=\frac{21}{2}$,
∴当n=$\frac{20}{2}=10$或n=$\frac{22}{2}=11$时,Sn取到最小值,
故答案为:10或11
点评 本题主要考查了等差数列的性质,考查了二次函数的图象与性质,是一道综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,可见部分信息如下,据此计算得到:参加数学抽测的人数n、分数在[90,100]内的人数分别为( )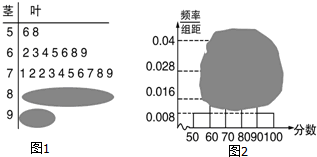

| A. | 25,2 | B. | 25,4 | C. | 24,2 | D. | 24,4 |
11. 执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
 执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )
执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |