题目内容
如图所示,在四面体P—ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=(1)证明PB⊥平面CEF;
(2)求二面角B-CE-F的大小.
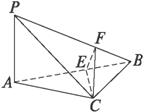
(1)证明:∵PA2+AC2=36+64=100=PC2,
∴△PAC是以∠PAC为直角的直角三角形,同理可证,
△PAB是以∠PAB为直角的直角三角形,△PCB是以∠PCB为直角的直角三角形.
故PA⊥平面ABC.
又∵S△PBC=![]() |PC||BC|=
|PC||BC|=![]() ×10×6=30,
×10×6=30,
而![]() |PB||CF|=
|PB||CF|=![]() ×
×![]() ×
×![]() =30=S△PBC.
=30=S△PBC.
故CF⊥PB.
又已知EF⊥PB,
∴PB⊥平面CEF.
(2)解:由(1)知PB⊥CE,PA⊥平面ABC,
∴AB是PB在平面ABC上的射影,故AB⊥CE.
在平面PAB内,过F作FF1垂直AB且交AB于F1点,则FF1⊥平面ABC,
EF1是EF在平面ABC上的射影,
∴EF⊥EC.
故∠FEB是二面角BCEF的平面角.
tan∠FEB=cot∠PBA=![]() .
.
故二面角BCEF的大小为arctan![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
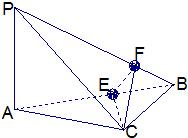 如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2
如图所示,在四面体P-ABC中,已知PA=BC=6,PC=AB=10,AC=8,PB=2 如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
如图所示,在四面体P-ABC中,PA⊥BC,PB⊥AC,BC=2,PB=PC,P-BC-A是60°的二面角.
 ,PB=10,F是线段PB上一点,
,PB=10,F是线段PB上一点, ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
 ,F是线段PB上一点,CF=
,F是线段PB上一点,CF=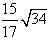 ,点E在线段AB上,且EF⊥PB,
,点E在线段AB上,且EF⊥PB, 