题目内容
等比数列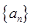 中,
中,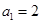 ,
, =4,函数
=4,函数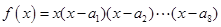 ,则
,则 ( )
( )
A.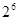 | B.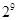 | C.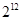 | D. |
C
解析试题分析:因为等比数列中首项为2,第八项为4,那么可以利用其通项公式得到q7=2,而
f(x)=x(x- )(x-
)(x- )…(x-
)…(x- ),故有f’(x)=x’[(x-
),故有f’(x)=x’[(x- )(x-
)(x- )…(x-
)…(x- )]+ x[(x-
)]+ x[(x- )(x-
)(x- )…(x-
)…(x- )]’=(-1)8
)]’=(-1)8


 +0=
+0=


 =
= ,故选C.
,故选C.
考点:本试题主要考查了等比数列的性质和函数的导数的运算的综合运用。
点评:解决该试题的关键是能理解f’(x)的表示的结果正确的表示,利用整体的思想来表示乘积的函数的导数。

练习册系列答案
相关题目
已知等比数列{an}公比为q,其前n项和为Sn,若S3,S9,S6成等差数列,则q3等于
A.- | B.1 | C.- 或1 或1 | D.-1或 |
三个数成等比数列,其和为14,各数平方和为84,则这三个数为( )
| A.2,4,8 | B.8,4,2 |
| C.2,4,8,或8,4,2 | D.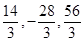 |
已知等比数列 中,有
中,有 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则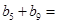 ( )
( )
| A.2 | B.4 | C.8 | D.16 |
已知递增等比数列 满足
满足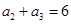 和
和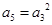 ,则
,则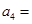
| A.1 | B.8 | C.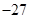 | D.8或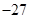 |
数列 满足
满足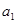 ,
,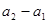 ,
, ,…,
,…,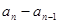 是首项为
是首项为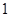 ,公比为
,公比为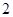 的等比数列,那么
的等比数列,那么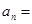 ( )
( )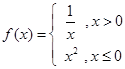
A.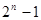 | B.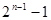  | C.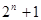 | D.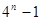 |
若x,2x+2,3x+3是一个等比数列的连续三项,则x的值为 ( )
| A.-4 | B.-1 | C.1或4 | D.-1或-4 |
在等比数列 中,
中, ,则
,则 =( )
=( )
A. | B. | C. | D. |
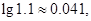
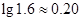 )
)