��Ŀ����
����Ŀ���ס�����λСѧ������2008����˼�������ޡ�5�������С�������������������������������ӭӭ���͡����ݸ�һ������������Ͷ��һ�����ӵķ�ʽ������Ϸ���������£����������ϵĵ���������ʱ����Ӯ����һ�����ޣ�������Ӯ�ü�һ�����ޣ��涨�����ӵĴ�����9��ʱ�����ڴ�ǰij����Ӯ�����и���ʱ��Ϸ��ֹ������Ϸ��ֹʱͶ�����ӵĴ���Ϊ��
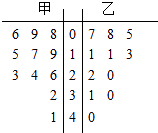
��1���������ӵĴ���Ϊ7�ĸ��ʣ�
��2����εķֲ��м���ѧ����E�Σ�
���𰸡�
��1���⣺����=7ʱ������Ӯ��ζ�š����ߴμ�Ӯ��ǰ6��Ӯ5�Σ�
�����ݹ���ǰ5���б���1�Ρ����ɹ���ÿ�μ�Ӯ����Ӯ�ĸ��ʾ�Ϊ ![]() ��
��
���P����=7��= ![]()
��2���⣺����Ϸ��ֹʱ�������ϵĵ������������ֵĴ���Ϊm��
���ϵĵ�����ż�����ֵĴ���Ϊn��
����  ���ɵã�
���ɵã�
��m=5��n=0��m=0��n=5ʱ����=5��
��m=6n=1��m=1��n=6ʱ����=7
��m=7��n=2��m=2��n=7ʱ����=9��
��˦εĿ���ȡֵ��5��7��9
ÿ��Ͷ����Ӯ����һ����������Ӯ�ü�һ�����Ŀ�������ͬ������ʶ��� ![]()
���Ԧεķֲ����ǣ� 
�� ![]() ��
��
�����������ڣ�1���������ӵĴ���Ϊ7�ĸ��ʣ����ȿ��Է����õ���Ӯ����Ӯ�ĸ��ʾ�Ϊ ![]() ������7�μ�Ӯ��ζ�š����ߴμ�Ӯ��ǰ6��Ӯ5�Σ������ݹ���ǰ5���б���1�Ρ�������Ӯͬ�����ʿɸ��ݶ���ֲ��г�ʽ����⼴�ɣ�
������7�μ�Ӯ��ζ�š����ߴμ�Ӯ��ǰ6��Ӯ5�Σ������ݹ���ǰ5���б���1�Ρ�������Ӯͬ�����ʿɸ��ݶ���ֲ��г�ʽ����⼴�ɣ�
���ڣ�2����εķֲ��м���ѧ����E�Σ��ʿ������������ֵĴ���Ϊm��ż�����ֵĴ���Ϊn��Ȼ����������г���ϵʽ��������ܵ�m n��ֵ�֦�=m+n������εĿ���ȡֵ��Ȼ��ֱ�������ʼ��ɵõ��εķֲ��У��ٸ���������ʽ���E�μ��ɣ�
�����㾫�������ڱ��⿼�����ɢ�������������ֲ��У���Ҫ�˽����������Ʒ����������У������������X����ȡ��ֵ�����ǿ���һ������һһ�г����������������������ɢ�������������ɢ����������ķֲ��У�һ���,����ɢ���������X����ȡ��ֵΪx1,x2,.....,xi,......,xn��Xȡÿһ��ֵ xi(i=1,2,......���ĸ���P(��=xi����Pi����Ʊ�Ϊ��ɢ���������X �ĸ��ʷֲ�����Ʒֲ��в��ܵó���ȷ�𰸣�