题目内容
(2012•泰安一模)(x3-
)4展开式中常数项为
| 1 | x |
-4
-4
.分析:利用二项展开式的通向公式Tr+1=
•(x3)4-r•(-
)r即可求得展开式中的常数项.
| C | r 4 |
| 1 |
| x |
解答:解:设(x3-
)4展开式的通项为Tr+1,则Tr+1=
•(x3)4-r•(-
)r=(-1)r•
•x12-4r•
令12-4r=0得r=3.
∴开式中常数项为:(-1)3•
=-4.
故答案为:-4.
| 1 |
| x |
| C | r 4 |
| 1 |
| x |
| C | r 4 |
令12-4r=0得r=3.
∴开式中常数项为:(-1)3•
| C | 3 4 |
故答案为:-4.
点评:本题考查二项式系数的性质,利用通项公式化简是关键,属于中档题.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
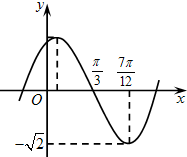 (2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则
(2012•泰安一模)函数f(x)=Asin(ωx+?)(A,ω,?为常数,A>0,ω>0)的部分图象如图所示,则