题目内容
(本小题满分13分)
已知数列{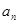 }满足
}满足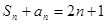 ,
,
(I)写出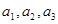 ,并推测
,并推测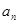 的表达式;
的表达式;
(II)用数学归纳法证明所得的结论。
(Ⅰ) 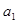 =
= ,
, 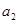 =
=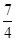 ,
, 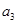 =
=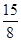 , 猜测
, 猜测 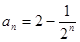 。(Ⅱ)见解析。
。(Ⅱ)见解析。
解析试题分析: (1)根据数列的前几项来归纳猜想得到结论。
(2)在第一问的基础上,进一步运用数学归纳法来加以证明即可。
解: (Ⅰ) 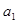 =
= ,
, 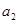 =
=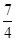 ,
, 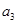 =
=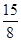 , 猜测
, 猜测 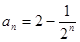 (4分)
(4分)
(Ⅱ) ①由(Ⅰ)已得当n=1时,命题成立;
②假设 时,命题成立,即
时,命题成立,即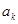 =2-
=2-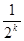 , (6分)
, (6分)
那么当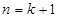 时,
时, 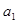 +
+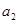 +……+
+……+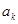 +2
+2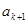 =2(k+1)+1,
=2(k+1)+1,
且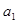 +
+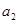 +……+
+……+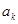 =2k+1-
=2k+1-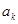 (8分)
(8分)
∴2k+1-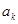 +2ak+1=2(k+1)+1=2k+3,
+2ak+1=2(k+1)+1=2k+3,
∴2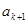 =2+2-
=2+2-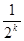 ,
, 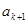 =2-
=2-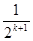 ,
,
即当n=k+1时,命题成立.
根据①②得n∈N+ , 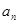 =2-
=2-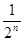 都成立 (13分)
都成立 (13分)
考点:本题主要考查了数列的归纳猜想思想的运用。以及运用数学归纳法求证结论的成立与否。
点评:解决该试题的关键是猜想的正确性,以及和运用数学归纳法证明命题时,要注意假设的运用,推理论证得到证明。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
设 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. | B.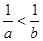 | C.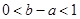 | D.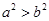 |
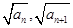 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(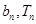 )在直线y=-
)在直线y=-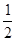 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。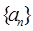 中,
中,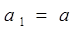 ,
, 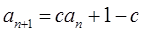
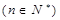
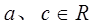
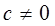
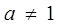 时,
时, 是等比数列,并求
是等比数列,并求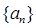 通项公式。
通项公式。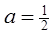 ,
,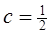 ,
,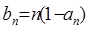
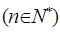 求:数列
求:数列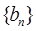 的前n项的和
的前n项的和 。
。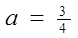 、
、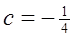 、
、 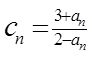 。记
。记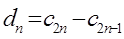 ,数列
,数列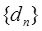 的前n项和
的前n项和 。证明:
。证明: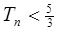
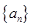 是等差数列,其中
是等差数列,其中 .
.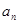 ;
;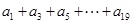 值.
值.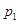 ,恰好
,恰好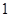 次正面向上的概率为
次正面向上的概率为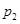 ;等比数列
;等比数列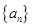 满足:
满足: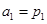 ,
,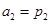
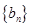 满足:
满足: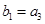 ,
,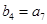 ,求等差数列
,求等差数列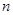 项和
项和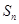 .
. 是等比数列
是等比数列 的公比
的公比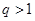 且
且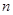 项的和。若
项的和。若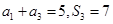 。(1)求数列
。(1)求数列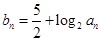 ,求数列
,求数列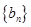 的前
的前 。
。 中,
中, ,
,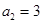 ,其前
,其前 项和
项和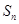 满足
满足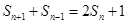 (
(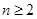 ,
,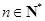 ).
).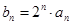 , 求数列
, 求数列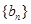 的前
的前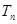 ;
;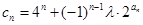 (
(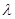 为非零整数,
为非零整数,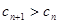 恒成立.
恒成立.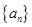 的前
的前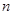 项和是
项和是 ,且
,且 .
.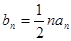 ,求数列
,求数列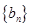 的前
的前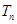 .
.