题目内容
手表的表面在一平面上.整点1,2,…,12这12个数字等间隔地分布在半径为1的圆周上.从整点i到整点i+1的向量记作![]() ,则
,则![]() •
•![]() +
+![]() •
•![]() +…+
+…+![]() •
•![]() = .
= .
考点:
平面向量数量积的运算;数列的求和.
专题:
压轴题;平面向量及应用.
分析:
把圆分成12份,每一份所对应的圆心角是30度,用余弦定理计算出每个向量的模的平方都是2﹣![]() ,而所求向量的夹角都是30度,求出其中一个数量积,乘以12个即得可到结果.
,而所求向量的夹角都是30度,求出其中一个数量积,乘以12个即得可到结果.
解答:
解::∵整点把圆分成12份,
∴每一份所对应的圆心角是30度,
连接相邻的两点组成等腰三角形底边平方为 2﹣![]() ,每对向量的夹角为30°,
,每对向量的夹角为30°,
每对向量的数量积为 ( 2﹣![]() )cos30°=
)cos30°=![]() ﹣
﹣![]() ,故
,故 ![]() •
•![]() +
+![]() •
•![]() +…+
+…+![]() •
•![]() =12(
=12( ![]() ﹣
﹣![]() )=
)=![]() ,
,
故答案为 ![]() .
.
点评:
本题是向量数量积的运算,条件中没有直接给出两个向量的模和两向量的夹角,只是题目所要的向量要应用圆的性质来运算,把向量的数量积同解析几何问题结合在一起,属于
中档题.

练习册系列答案
相关题目
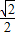 的圆周上,从整点i到整点(i+1)的向量记作
的圆周上,从整点i到整点(i+1)的向量记作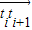 ,则
,则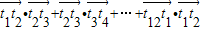 = .
= .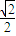 的圆周上,从整点i到整点(i+1)的向量记作
的圆周上,从整点i到整点(i+1)的向量记作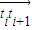 ,则
,则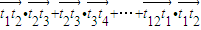 = .
= .