题目内容
已知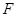 为抛物线
为抛物线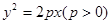 的焦点,点
的焦点,点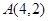 为抛物线内一定点,点
为抛物线内一定点,点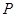 为抛物线上一动点,
为抛物线上一动点,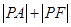 最小值为8.
最小值为8.
(1)求该抛物线的方程;
(2)若直线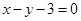 与抛物线交于
与抛物线交于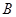 、
、 两点,求
两点,求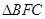 的面积.
的面积.
(1) .(2)
.(2)
解析试题分析:(1)设 为点
为点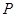 到
到 的距离,则由抛物线定义,
的距离,则由抛物线定义, ,
,
所以当点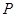 为过点
为过点 且垂直于准线的直线与抛物线的交点时,
且垂直于准线的直线与抛物线的交点时, 取得最小值,即
取得最小值,即 ,解得
,解得
∴抛物线的方程为 .
.
(2)设 ,联立
,联立 得
得 ,
,
显然 ,
,
 ,
,
 .
.
又
 到直线
到直线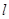 的距离为
的距离为 ,
,
考点:本题主要考查抛物线的定义,直线与抛物线的位置关系,点到直线的距离公式,三角形面积公式。
点评:中档题,涉及“抛物线内一定点,点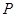 为抛物线上一动点,求
为抛物线上一动点,求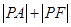 最小值”问题,往往利用抛物线定义,“化折为直”。涉及抛物线与直线位置关系问题,往往利用韦达定理。
最小值”问题,往往利用抛物线定义,“化折为直”。涉及抛物线与直线位置关系问题,往往利用韦达定理。

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 中,点
中,点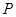 到两点
到两点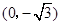 ,
, 的距离之和等于4,设点
的距离之和等于4,设点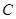 .
. 与
与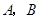 两点.k为何值时
两点.k为何值时
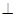
 ?此时
?此时 的值是多少?
的值是多少? 的离心率
的离心率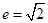 且点
且点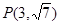 在双曲线C上.
在双曲线C上.  求直线l的方程.
求直线l的方程.  (
( )的准线与
)的准线与 轴交于
轴交于 ,焦点为
,焦点为 ;以
;以 的椭圆
的椭圆 与抛物线
与抛物线 在
在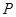 .
.
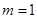 时,求椭圆的方程;
时,求椭圆的方程; 经过椭圆
经过椭圆 、
、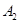 ,如果以线段
,如果以线段 为直径作圆,试判断点
为直径作圆,试判断点 ,使得
,使得 的边长是连续的自然数,若存在,求出这样的实数
的边长是连续的自然数,若存在,求出这样的实数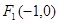 及
及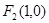 ,点
,点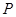 在以
在以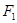 、
、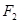 为焦点的椭圆
为焦点的椭圆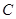 上,且
上,且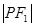 、
、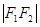 、
、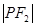 构成等差数列.
构成等差数列.
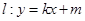 与椭圆
与椭圆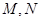 是直线
是直线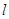 上的两点,且
上的两点,且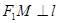 ,
,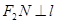 . 求四边形
. 求四边形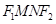 面积
面积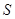 的最大值.
的最大值.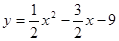 与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
与x轴交于A、B两点,与y轴交于点C,连接BC、AC。
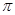 )。
)。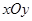 中,
中,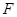 是抛物线
是抛物线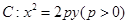 的焦点,
的焦点,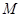 是抛物线
是抛物线 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过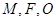 三点的圆的圆心为
三点的圆的圆心为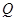 ,点
,点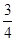 .
.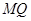 与抛物线
与抛物线 .
.
 所成的比为2,求线段AB所在直线的方程.
所成的比为2,求线段AB所在直线的方程.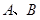 ,
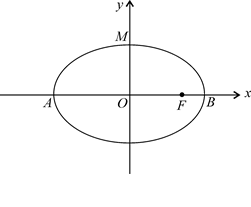
,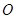 为椭圆中心,
为椭圆中心,
 为椭圆的右焦点,
为椭圆的右焦点,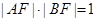 ,
,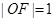 .
.
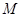 ,直线
,直线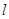 交椭圆于
交椭圆于 两点,问:是否存在直线
两点,问:是否存在直线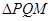 的垂心?若存在,求出直线
的垂心?若存在,求出直线