题目内容
已知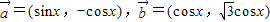 ,函数
,函数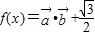 .
.(1)求f(x)的最小正周期,并求其图象对称中心的坐标;
(2)当
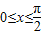 时,求函数f(x)的值域.
时,求函数f(x)的值域.
【答案】分析:(1)由向量的坐标运算可求得f(x)=sin(2x-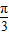 ),从而可求f(x)的最小正周期,并求其图象对称中心的坐标;
),从而可求f(x)的最小正周期,并求其图象对称中心的坐标;
(2)由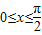 可得2x-
可得2x-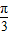 ∈[-
∈[-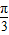 ,
,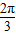 ],从而可求得函数f(x)的值域.
],从而可求得函数f(x)的值域.
解答:解:(1)∵f(x)=sinxcosx-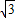 cos2x+
cos2x+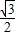
= sin2x-
sin2x-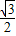 (cos2x+1)+
(cos2x+1)+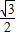
= sin2x-
sin2x-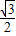 cos2x
cos2x
=sin(2x-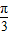 ) …(2分)
) …(2分)
∴f(x)的最小正周期为π,
令sin(2x-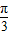 )=0,,得2x-
)=0,,得2x-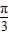 =kπ,
=kπ,
∴x=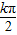 +
+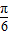 ,(k∈Z).
,(k∈Z).
故所求对称中心的坐标为(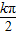 +
+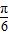 ,0),(k∈Z)-…(4分)
,0),(k∈Z)-…(4分)
(2)∵0≤x≤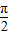 ,∴-
,∴-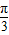 <2x-
<2x-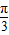 ≤
≤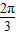 …(6分)
…(6分)
∴-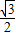 ≤sin(2x-
≤sin(2x-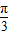 )≤1,
)≤1,
即f(x)的值域为[-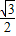 ,1]…(8分)
,1]…(8分)
点评:本题考查平面向量数量积的运算,考查两角和与差的正弦函数,考查正弦函数的定义域和值域及其周期,属于三角中的综合,考查分析问题、解决问题的能力.
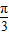 ),从而可求f(x)的最小正周期,并求其图象对称中心的坐标;
),从而可求f(x)的最小正周期,并求其图象对称中心的坐标;(2)由
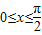 可得2x-
可得2x-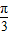 ∈[-
∈[-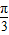 ,
,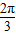 ],从而可求得函数f(x)的值域.
],从而可求得函数f(x)的值域.解答:解:(1)∵f(x)=sinxcosx-
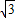 cos2x+
cos2x+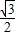
=
 sin2x-
sin2x-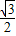 (cos2x+1)+
(cos2x+1)+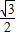
=
 sin2x-
sin2x-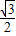 cos2x
cos2x=sin(2x-
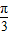 ) …(2分)
) …(2分)∴f(x)的最小正周期为π,
令sin(2x-
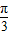 )=0,,得2x-
)=0,,得2x-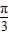 =kπ,
=kπ,∴x=
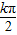 +
+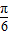 ,(k∈Z).
,(k∈Z).故所求对称中心的坐标为(
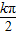 +
+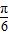 ,0),(k∈Z)-…(4分)
,0),(k∈Z)-…(4分)(2)∵0≤x≤
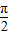 ,∴-
,∴-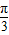 <2x-
<2x-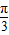 ≤
≤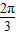 …(6分)
…(6分)∴-
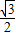 ≤sin(2x-
≤sin(2x-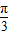 )≤1,
)≤1,即f(x)的值域为[-
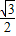 ,1]…(8分)
,1]…(8分)点评:本题考查平面向量数量积的运算,考查两角和与差的正弦函数,考查正弦函数的定义域和值域及其周期,属于三角中的综合,考查分析问题、解决问题的能力.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
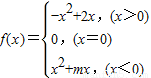 ,
, ;
; 的图象;
的图象; 在区间[-1,|
在区间[-1,| |-2]上单调递增,试确定
|-2]上单调递增,试确定 .
. 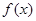 的最小正周期和当
的最小正周期和当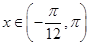 时的值域;
时的值域;
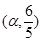 ,
,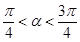 .求
.求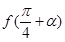 的值.
的值. .
. 的值;
的值; ,
, ,求
,求 的值.
的值. ,函数
,函数 .
. 的单调递减区间;
的单调递减区间; 在区间
在区间 上有极值,求
上有极值,求 的取值范围;
的取值范围;