题目内容
在△ABC中,AB=2,AC=3, •
•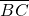 =1,则BC=
=1,则BC=
- A.

- B.

- C.2

- D.
A
分析:设∠B=θ,由 •
• =1,利用平面向量的数量积运算法则列出关系式,表示出cosθ,再利用余弦定理表示出cosθ,两者相等列出关于BC的方程,求出方程的解即可得到BC的长.
=1,利用平面向量的数量积运算法则列出关系式,表示出cosθ,再利用余弦定理表示出cosθ,两者相等列出关于BC的方程,求出方程的解即可得到BC的长.
解答:根据题意画出相应的图形,如图所示:

∵ •
• =1,设∠B=θ,AB=2,
=1,设∠B=θ,AB=2,
∴2•BC•cos(π-θ)=1,即cosθ=- ,
,
又根据余弦定理得:cosθ= =
= ,
,
∴- =
= ,即BC2=3,
,即BC2=3,
则BC= .
.
故选A
点评:此题属于解三角形的题型,涉及的知识有:平面向量的数量积运算,余弦定理,以及诱导公式的运用,熟练掌握定理及法则是解本题的关键.
分析:设∠B=θ,由
 •
• =1,利用平面向量的数量积运算法则列出关系式,表示出cosθ,再利用余弦定理表示出cosθ,两者相等列出关于BC的方程,求出方程的解即可得到BC的长.
=1,利用平面向量的数量积运算法则列出关系式,表示出cosθ,再利用余弦定理表示出cosθ,两者相等列出关于BC的方程,求出方程的解即可得到BC的长.解答:根据题意画出相应的图形,如图所示:

∵
 •
• =1,设∠B=θ,AB=2,
=1,设∠B=θ,AB=2,∴2•BC•cos(π-θ)=1,即cosθ=-
 ,
,又根据余弦定理得:cosθ=
 =
= ,
,∴-
 =
= ,即BC2=3,
,即BC2=3,则BC=
 .
.故选A
点评:此题属于解三角形的题型,涉及的知识有:平面向量的数量积运算,余弦定理,以及诱导公式的运用,熟练掌握定理及法则是解本题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目