题目内容
是否存在常数a、b、c,使等式(
解:令n=1,n=2,n=3,得
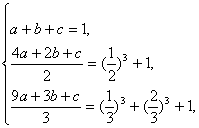
解得a=![]() ,b=
,b=![]() ,c=
,c=![]() .
.
下面用数学归纳法证明(![]() )3+(
)3+(![]() )3+…+(
)3+…+(![]() )3=
)3=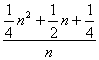 .
.
(1)当n=1时由上面求解过程可知等式成立.
(2)假设当n=k时,等式成立,即(![]() )3+(
)3+(![]() )3+…+(
)3+…+(![]() )3=
)3=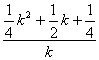 .
.
当n=k+1时,(![]() )3+(
)3+(![]() )3+…+(
)3+…+(![]() )3
)3
=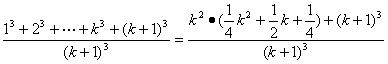
=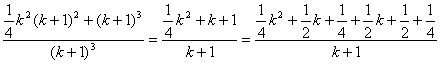
=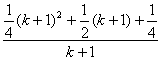 ,
,
即n=k+1时等式成立.
由(1)(2)知,对任意n∈N*等式(![]() )3+(
)3+(![]() )3+…+(
)3+…+(![]() )3=
)3=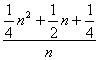 成立,
成立,
即存在a=![]() ,b=
,b=![]() ,c=
,c=![]() 使原等式成立.
使原等式成立.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目