题目内容
若球的一个截面的面积是36π,且截面到球心的距离为8,则这个球的表面积为
400π
400π
.分析:根据圆的面积公式算出截面圆的半径r=6,再由截面到球心的距离为d=8,利用球的截面圆性质与勾股定理算出球的半径R=10,即可得到这个球的表面积.
解答:解:设球的半径为R,截面圆的半径为r,
∵截面的面积是36π,
∴πr2=36π,可得r=6.
又∵截面到球心的距离为d=8,
∴根据球的截面圆性质,可得R=
=
=10
由此可得这个球的表面积为S=4πR2=400π.
故答案为:400π

∵截面的面积是36π,
∴πr2=36π,可得r=6.
又∵截面到球心的距离为d=8,
∴根据球的截面圆性质,可得R=
| d2+r2 |
| 82+62 |
由此可得这个球的表面积为S=4πR2=400π.
故答案为:400π
点评:本题已知距离球心的距离等于8的球的截面圆的面积为36π,求球的表面积.着重考查了球的截面圆性质、勾股定理与球的表面积公式等知识,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
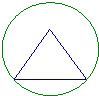 棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是( )
棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(正四面体的截面)的面积是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
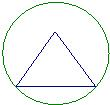
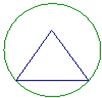 一个三棱锥的棱长均为2,四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(三棱锥的截面)的面积是( )
一个三棱锥的棱长均为2,四个顶点都在同一个球面上,若过该球球心的一个截面如图,则图中三角形(三棱锥的截面)的面积是( )