题目内容
等比数列{an}的各项均为正数,且a5a6+a3a8=16,则log2a1+log2a2+…+log2a10的值为
- A.15
- B.-15
- C.3
- D.-3
A
分析:由条件并利用等比数列的定义和性质可得8=a1a10,把要求的式子化为log2(a1a2…a10)=log2(a1a10)5,运算求出结果.
解答:等比数列{an}的各项均为正数,且a5a6+a3a8=16,则 a5a6 =a3a8 =8=a1a10.
∴log2a1+log2a2+…+log2a10=log2(a1a2…a10)=log2(a1a10)5=log2215=15.
故选A.
点评:本题主要考查对数的运算性质,以及等比数列的定义和性质的应用,求出 8=a1a10,是解题的关键,属于中档题.
分析:由条件并利用等比数列的定义和性质可得8=a1a10,把要求的式子化为log2(a1a2…a10)=log2(a1a10)5,运算求出结果.
解答:等比数列{an}的各项均为正数,且a5a6+a3a8=16,则 a5a6 =a3a8 =8=a1a10.
∴log2a1+log2a2+…+log2a10=log2(a1a2…a10)=log2(a1a10)5=log2215=15.
故选A.
点评:本题主要考查对数的运算性质,以及等比数列的定义和性质的应用,求出 8=a1a10,是解题的关键,属于中档题.

练习册系列答案
相关题目
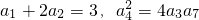 ,则数列{an}的通项公式为________.
,则数列{an}的通项公式为________. ,则数列{an}的通项公式为 .
,则数列{an}的通项公式为 .