题目内容
给出命题:①若函数y=f(2x-1)为偶函数,则y=f(2x)的图象关于x=
 对称;
对称;②把函数
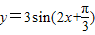 的图象向右平移
的图象向右平移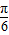 得到y=3sin2x的图象
得到y=3sin2x的图象③函数
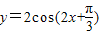 的图象关于点
的图象关于点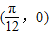 对称;
对称;④函数y=sin|x|是周期函数,且周期为2π;
⑤△ABC中,若sinA,sinB,sinC成等差数列,则
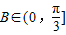 .
.其中正确命题所有的序号是 .
【答案】分析:①函数y=f(2x-1)为偶函数,可知f(x)关于y轴对称,根据平移的性质进行判断;
②根据三角函数平移的性质进行判断;
③把点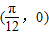 代入函数
代入函数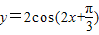 进行判断;
进行判断;
④已知y=sin|x|是周期函数,且又是偶函数,从而进行判断;
⑤△ABC中,若sinA,sinB,sinC成等差数列,可得2sinB=sinC+sinA,根据正弦定理进行求解;
解答:解:①函数y=f(2x-1)为偶函数,关于y轴对称,将其向左平移 个单位可得y=f(2x),其对称轴为x=-
个单位可得y=f(2x),其对称轴为x=- ,故①错误;
,故①错误;
②函数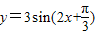 的图象向右平移
的图象向右平移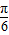 得y=3sin(2x-
得y=3sin(2x-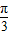 +
+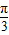 )=3sin2x,故②正确;
)=3sin2x,故②正确;
③函数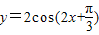 ,当x=
,当x=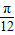 时,y=2cos
时,y=2cos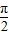 =0,故③正确;
=0,故③正确;
④函数y=sin|x|,它是偶函数,不是周期函数,故④错误;
⑤∵⑤△ABC中,若sinA,sinB,sinC成等差数列,可得2sinB=sinC+sinA,可得2b=a+c,
∴cosB=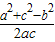 =
=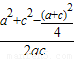 =
=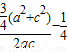 ≥
≥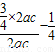 =
= ,
,
∴cosB≥ ,B∈(0,π),
,B∈(0,π),
∴B∈(0,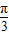 ],故⑤正确;
],故⑤正确;
故答案为②③⑤;
点评:本题考查三角函数的周期性及其求法,正弦函数的对称性,正切函数的单调性,考查基本概念的掌握程度,是基础题.
②根据三角函数平移的性质进行判断;
③把点
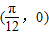 代入函数
代入函数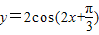 进行判断;
进行判断;④已知y=sin|x|是周期函数,且又是偶函数,从而进行判断;
⑤△ABC中,若sinA,sinB,sinC成等差数列,可得2sinB=sinC+sinA,根据正弦定理进行求解;
解答:解:①函数y=f(2x-1)为偶函数,关于y轴对称,将其向左平移
 个单位可得y=f(2x),其对称轴为x=-
个单位可得y=f(2x),其对称轴为x=- ,故①错误;
,故①错误;②函数
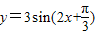 的图象向右平移
的图象向右平移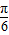 得y=3sin(2x-
得y=3sin(2x-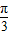 +
+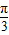 )=3sin2x,故②正确;
)=3sin2x,故②正确;③函数
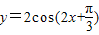 ,当x=
,当x=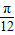 时,y=2cos
时,y=2cos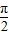 =0,故③正确;
=0,故③正确;④函数y=sin|x|,它是偶函数,不是周期函数,故④错误;
⑤∵⑤△ABC中,若sinA,sinB,sinC成等差数列,可得2sinB=sinC+sinA,可得2b=a+c,
∴cosB=
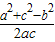 =
=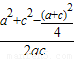 =
=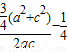 ≥
≥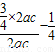 =
= ,
,∴cosB≥
 ,B∈(0,π),
,B∈(0,π),∴B∈(0,
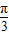 ],故⑤正确;
],故⑤正确;故答案为②③⑤;
点评:本题考查三角函数的周期性及其求法,正弦函数的对称性,正切函数的单调性,考查基本概念的掌握程度,是基础题.

练习册系列答案
相关题目