题目内容
(1)、已知函数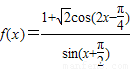 .若角
.若角 .
.(2)函数
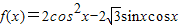 的图象按向量
的图象按向量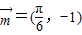 平移后,得到一个函数g(x)的图象,求g(x)的解析式.
平移后,得到一个函数g(x)的图象,求g(x)的解析式.
【答案】分析:(1)通过角的范围求出sinα,利用两角和与二倍角公式和诱导公式化简函数的表达式,求出函数的值.
(2)利用二倍角公式化简函数的表达式,然后按照向量平移,即可求出所求函数的解析式.
解答:解:(1)由已知条件,得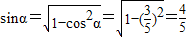 .…(2分)
.…(2分)
所以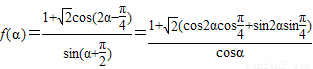 …(6分)
…(6分)
=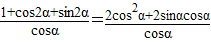 …(9分)
…(9分)
=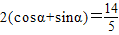 .…(10分)
.…(10分)
(2)函数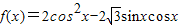 =cos2x-
=cos2x-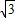 sin2x+1=2cos(2x+
sin2x+1=2cos(2x+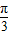 )+1;
)+1;
函数图象按向量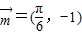 平移后,得到一个函数g(x)=2cos[2(x-
平移后,得到一个函数g(x)=2cos[2(x-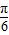 )+
)+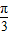 ]-1+1=2cos2x的图象,
]-1+1=2cos2x的图象,
故函数的解析式为:g(x)=2cos2x.
点评:本题考查三角函数的化简,同角三角函数的基本关系式的应用,二倍角公式的应用,函数的图象的平移,考查计算能力.
(2)利用二倍角公式化简函数的表达式,然后按照向量平移,即可求出所求函数的解析式.
解答:解:(1)由已知条件,得
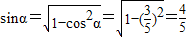 .…(2分)
.…(2分)所以
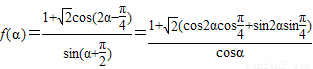 …(6分)
…(6分)=
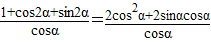 …(9分)
…(9分)=
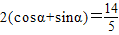 .…(10分)
.…(10分)(2)函数
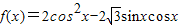 =cos2x-
=cos2x-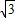 sin2x+1=2cos(2x+
sin2x+1=2cos(2x+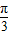 )+1;
)+1;函数图象按向量
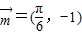 平移后,得到一个函数g(x)=2cos[2(x-
平移后,得到一个函数g(x)=2cos[2(x-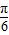 )+
)+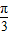 ]-1+1=2cos2x的图象,
]-1+1=2cos2x的图象,故函数的解析式为:g(x)=2cos2x.
点评:本题考查三角函数的化简,同角三角函数的基本关系式的应用,二倍角公式的应用,函数的图象的平移,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
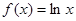 ,若
,若
 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上有两个零点,求实数b的取值范围;
上有两个零点,求实数b的取值范围;
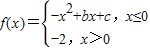 ,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .
,若f(-1)=1,f(0)=-2,则函数g(x)=f(x)+x的零点个数为 .