题目内容
(本小题满分12分)设二次函数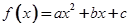 在区间
在区间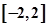 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合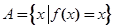 .
.
(Ⅰ)若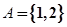 ,且
,且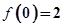 ,求M和m的值;
,求M和m的值;
(Ⅱ)若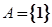 ,且
,且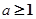 ,记
,记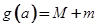 ,求
,求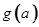 的最小值.
的最小值.
【答案】
(1)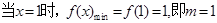 ;
;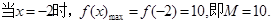
(2)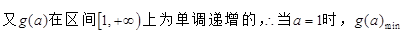 =
=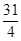 。
。
【解析】(1) 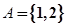 ,可知
,可知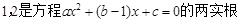 ,从而根据韦达定理可建立关于a,b的方程,解出a,b的值.f(x)的解析式确定,再利用二次函数求最值的方法求其最值.
,从而根据韦达定理可建立关于a,b的方程,解出a,b的值.f(x)的解析式确定,再利用二次函数求最值的方法求其最值.
(2)解本小题的关键是根据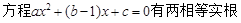 :x=1,从而利用韦达定理可建立a,b,c两个方程,用a分别表示b,c,代入f(x),再讨论二次函数的对称轴,确定其最值即可.
:x=1,从而利用韦达定理可建立a,b,c两个方程,用a分别表示b,c,代入f(x),再讨论二次函数的对称轴,确定其最值即可.
解:(1)由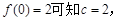 又
又
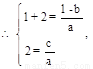
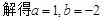
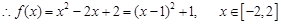
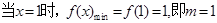 ;
;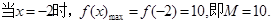 …6分
…6分
(2)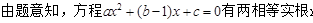 x=1
x=1
∴ 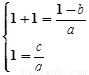 , 即
, 即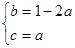 ∴f(x)=ax2+(1-2a)x+a, x∈[-2,2]
∴f(x)=ax2+(1-2a)x+a, x∈[-2,2]
其对称轴方程为x=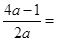
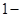
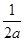 又a≥1,故1-
又a≥1,故1-
∴M=f(-2)=9a-2 m=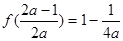 g(a)=M+m=9a-
g(a)=M+m=9a-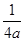 -1
-1
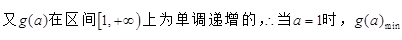 =
=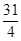 ………………12分
………………12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目