题目内容
已知函数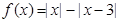
(1)解关于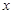 的不等式
的不等式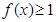 ;
;
(2)若存在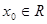 ,使得
,使得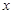 的不等式
的不等式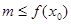 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2)
解析试题分析:(1)先去掉绝对值得到 ,然后遂个求解不等式
,然后遂个求解不等式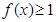 最终可得解集
最终可得解集 ;(2)利用含参不等式的求解方法先确定
;(2)利用含参不等式的求解方法先确定 因为
因为 所以
所以 则
则 .
.
试题解析:(1)原不等式等价于①: 1分
1分
或②: 2分 或③:
2分 或③: 3分
3分
解不等式组①无解; 4分 解不等式组②得: 5分
5分
解不等式组③得: 6分
6分
所以原不等式的解集为 7分;
7分;
(2)依题意 9分
9分
因为 ,所以
,所以 11分
11分
所以 , 12分
, 12分
所以实数 的取值范围为
的取值范围为 13分.
13分.
考点:1,分段函数2,含参函数不等式的求解.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 的两侧,则a的取值范围是____ _。
的两侧,则a的取值范围是____ _。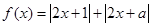
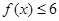 的解集;
的解集;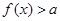 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围 .
.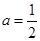 时,解不等式
时,解不等式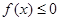 ;
; ,解关于
,解关于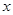 的不等式
的不等式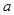 2+
2+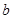 2恒成立,试求2
2恒成立,试求2 的不等式
的不等式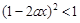 .
. 的一元二次不等式
的一元二次不等式 .
. 的解集是 .
的解集是 . 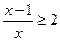 的解集是
的解集是