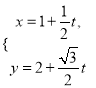[题目]已知正四棱柱的底面边长为.高为.现从该正四棱柱的个顶点中任取个点.设随机变量的值为以取出的个点为顶点的三角形的面积.(1)求概率,(2)求的分布列.并求其数学期望题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知正四棱柱的底面边长为，高为，现从该正四棱柱的个顶点中任取个点.设随机变量的值为以取出的个点为顶点的三角形的面积.

（1）求概率；

（2）求的分布列，并求其数学期望

【答案】见解析

【解析】

（1）因为正四棱柱的底面边长为，高为，

所以面积为的三角形的个点为顶点只能是同一底面上的顶点，共有个.

因此……………4分

（2）显然题设三角形三边不可能都是正四棱柱的棱.

①若三角形中恰有两边为正四棱柱的棱，另一边为底面对角线时，由（1）知，；若三角形中恰有两边为正四棱柱的棱，另一边为侧面对角线时，且

②若三角形中恰有一边为正四棱柱底面的棱时，且

若三角形中恰有一边为正四棱柱侧棱时，且

③若三角形中的边都不是正四棱柱的棱，则三边中两条为侧面对角线，一条为底面对角线.于是且

所以随机变量的分布列是

因此……………10分

练习册系列答案

相关题目

【题目】在平面直角坐标系xOy中，椭圆C的参数方程为（θ为参数），直线l的参数方程为（t为参数）．

（Ⅰ）写出椭圆C的普通方程和直线l的倾斜角；

（Ⅱ）若点P（1，2），设直线l与椭圆C相交于A，B两点，求|PA|·|PB|的值．

【题目】设函数f（x）＝|x－1|＋|2x－1|．

（Ⅰ）若对x＞0，不等式f（x）≥tx恒成立，求实数t的最大值M；

（Ⅱ）在（Ⅰ）成立的条件下，正实数a，b满足a2＋b2＝2M．证明：a＋b≥2ab．

【题目】如图，过椭圆：的左右焦点分别作直线，交椭圆于与，且.

（1）求证：当直线的斜率与直线的斜率都存在时，为定值；

（2）求四边形面积的最大值.

【题目】某市为了制定合理的节电方案，供电局对居民用电进行了调查，通过抽样，获得了某年200户居民每户的月均用电量（单位：度），将数据按照，，，，，，，，分成9组，制成了如图所示的频率分布直方图．

（Ⅰ）求直方图中的值并估计居民月均用电量的中位数；

（Ⅱ）现从第8组和第9组的居民中任选取2户居民进行访问，则两组中各有一户被选中的概率．

【题目】解关于x的方程：
（1）lgx+lg（x﹣3）=1；
（2）．

【题目】已知向量=（2cos， sin），=（cos，2cos），（ω＞0），设函数f（x）=，且f（x）的最小正周期为π．

（1）求函数f（x）的表达式；

（2）求f（x）的单调递增区间．

【题目】已知函数f（x）=loga（1﹣x）+loga（x+3），其中0＜a＜1．
（1）求函数f（x）的定义域；
（2）若函数f（x）的最小值为﹣4，求a的值．

【题目】已知以点A(－1,2)为圆心的圆与直线l1：x＋2y＋7＝0相切．过点B(－2,0)的动直线l与圆A相交于M，N两点，Q是MN的中点．

(1)求圆A的方程；

(2)当|MN|＝2时，求直线l的方程．

试题分类