Question

已知函数f(x)=1(a＞0且a≠1)

    在(-∞，+∞)上的奇函数．

    (Ⅰ)求a的值；

    (Ⅱ)求函数f(x)的值域；

    (Ⅲ)当x∈(0，1]时，tf(x)≥2^x-2恒成立，t的取值范围．

Answer 1

答案：解：(1)∵f(x)是定义在(-∞，+∞)上的奇函数，

即f(-x)=-f(x)，

令x=0得f(0)=1-=0，

解得a=2．

(Ⅱ)记y=f(x)，即y=，

∴2^x=，由2^x＞0知＞0，

∴-1＜y＜1即f(x)的值域为(-1，1)．

(Ⅲ)原不等式tf(x)≥2^x-2即≥2^x-2．

即：(2^x)²-(t+1)·2^x+t-2≤0．

设2^x=u，∵x∈(0，1]，∴u∈(1，2]．

∴x∈(0，1]时tf(x)≥2^x-2恒成立，即为u∈(1，2]时u²-(t+1)·u+t-20恒成立.

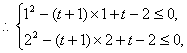
解得t≥0．

另解：(Ⅱ)∵f(x)=，

而2^x＞0，∴2^x+1＞1，∴0＜＜2，

∴-1＜1-＜1，即-1＜f(x)＜1．

∴f(x)的值域为(-1，1)．

(Ⅲ)∵x∈(0，1]，∴2^x-1＞0，

∴原式变为t≥·(2^x-2)==(2^x-1)-+1．

令μ=2^x-1，则μ∈(0，1]，原式变为t≥μ-+1.

而g(μ)=μ-+1在μ∈(0，1]时是增函数，

∴当μ=1时，g(μ)_max=0．

∴t≥0．