题目内容
(设函数f(x)=|x+a|-|x-4|,x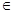 R
R
(1)当a=1时,解不等式f(x)<2;
(2)若关于x的不等式f(x)≤5-|a+l|恒成立,求实数a的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:本题主要考查绝对值不等式的解法、不等式的性质及恒成立问题等数学知识,考查学生的转化能力和计算能力.第一问,将函数化为分段函数,再解不等式;第二问,利用不等式的性质先求 的最大值,再解
的最大值,再解 这个绝对值不等式即可.
这个绝对值不等式即可.
试题解析:①∵ ,
,
∴由 得
得 .(4分)
.(4分)
②因为 ,
,
要使 恒成立,须使
恒成立,须使 ,
,
即 ,解得
,解得 .(7分)
.(7分)
考点:1.绝对值不等式的解法;2.不等式的性质.

练习册系列答案
相关题目
对任意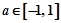 ,函数
,函数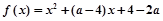 的值恒大于0,则x的范围是( )
的值恒大于0,则x的范围是( )
A. 或 或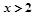 | B.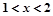 | C. 或 或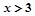 | D.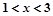 |


 ,对满足
,对满足 的一切实数
的一切实数 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 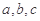 为三角形
为三角形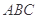 的三边,求证:
的三边,求证: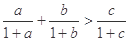
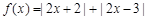 .
.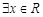 ,使得不等式
,使得不等式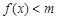 成立,求
成立,求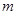 的取值范围;
的取值范围;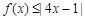 成立的
成立的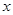 的取值范围.
的取值范围. .
.
 .
. 的不等式
的不等式 的解集为
的解集为 则实数
则实数 的取值范围是_________
的取值范围是_________
 与
与 的大小.
的大小.