题目内容
设函数f(x)=lnx,g(x)=ax+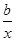 ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.
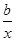 ,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.
,函数f(x)的图像与x轴的交点也在函数g(x)的图像上,且在此点处f(x)与g(x)有公切线.(Ⅰ)求a、b的值;
(Ⅱ)设x>0,试比较f(x)与g(x)的大小.
 (11)见解析
(11)见解析第一问解:因为f(x)=lnx,g(x)=ax+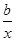
则其导数为
由题意得,
第二问,由(I)可知 ,令
,令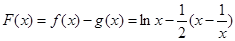 。
。
∵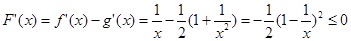 , …………8分
, …………8分
∴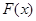 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当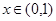 时,
时, ,有
,有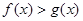 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时,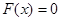 ,有
,有
解:因为f(x)=lnx,g(x)=ax+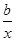
则其导数为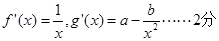
由题意得,
(11)由(I)可知 ,令
,令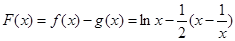 。
。
∵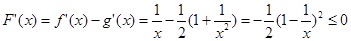 , …………8分
, …………8分
∴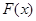 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分
∴当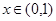 时,
时, ,有
,有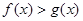 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时,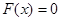 ,有
,有
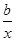
则其导数为

由题意得,

第二问,由(I)可知
 ,令
,令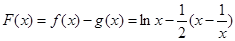 。
。∵
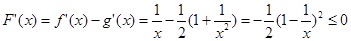 , …………8分
, …………8分∴
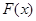 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分∴当
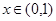 时,
时, ,有
,有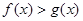 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时,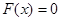 ,有
,有解:因为f(x)=lnx,g(x)=ax+
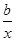
则其导数为
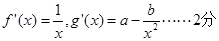
由题意得,

(11)由(I)可知
 ,令
,令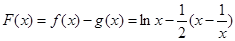 。
。∵
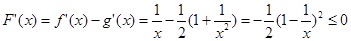 , …………8分
, …………8分∴
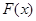 是(0,+∞)上的减函数,而F(1)=0, …………9分
是(0,+∞)上的减函数,而F(1)=0, …………9分∴当
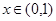 时,
时, ,有
,有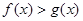 ;当
;当 时,
时, ,有
,有 ;当x=1时,
;当x=1时,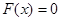 ,有
,有

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
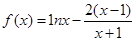 。
。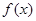 的单调性;
的单调性;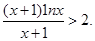
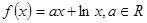
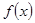 的极值;
的极值;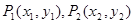 ,如果存在曲线上的点
,如果存在曲线上的点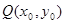 ,且
,且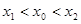 ,使得曲线在点
,使得曲线在点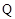 处的切线
处的切线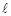 ∥
∥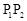 ,则称
,则称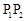 的伴随切线。特别地,当
的伴随切线。特别地,当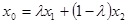 ,
,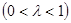 时,又称
时,又称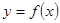 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;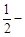 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。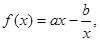 曲线
曲线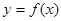 在点
在点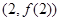 处的切线方程为
处的切线方程为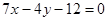 .
.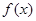 的解析式;
的解析式;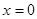 及直线
及直线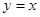 所围成的三角形的面积是一个定值,并求此定值.
所围成的三角形的面积是一个定值,并求此定值.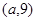 在函数
在函数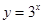 的图象上,则
的图象上,则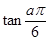 的值为
的值为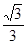
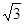
 对
对 且
且 恒有
恒有 ,则使
,则使 成立的实数
成立的实数 的取值范围是___▲___.
的取值范围是___▲___. .
. 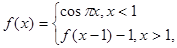 则
则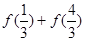 的值等于____▲
的值等于____▲