题目内容
 如图,两县城A和B相距20km,O为AB的中点,现要在以O为圆心、20km为半径的圆弧
如图,两县城A和B相距20km,O为AB的中点,现要在以O为圆心、20km为半径的圆弧 | MN |
(I)写出x关于θ的函数关系,并求该函数的定义域和值域;
(II)当x为多少km时,总影响度最小?
分析:(I)根据在三角形中应用余弦定理做出变量的表示式,得到一个关于三角函数的解析式,根据三角函数的性质做出函数的定义域和值域.
(II)根据余弦定理表示出要求的量,根据上一问的结果,得到变量的表示式,对函数求导,使得导函数大于0,小于0,求出函数的单调区间,得到最值,说明最值的实际意义.
(II)根据余弦定理表示出要求的量,根据上一问的结果,得到变量的表示式,对函数求导,使得导函数大于0,小于0,求出函数的单调区间,得到最值,说明最值的实际意义.
解答:解:(I)在△POA中,有余弦定理得:
x2=400+100-2×20×10cosθ=500-400cosθ
∴x=10
定义域为[
],值域为[10
,10
]
(II)在△POA中,有余弦定理得:
PB2=400+100-2×20×10cos(π-θ)=500+400cosθ
∵由(I)知400cosθ=500-x2,
∴PB2=1000-x2
∴y=
+
∴y′=
∵10
≤x≤10
,
令y′=0
得x=10
当10
≤x≤10
时,y′<0
当10
≤x≤10
,y′>0
∴当x=10
时,y取极小值也是最大值.
即当AP为10
时,总影响度最小.
x2=400+100-2×20×10cosθ=500-400cosθ
∴x=10
| 5-4cosθ |
定义域为[
| π |
| 3 |
| 2π |
| 3 |
| 3 |
| 7 |
(II)在△POA中,有余弦定理得:
PB2=400+100-2×20×10cos(π-θ)=500+400cosθ
∵由(I)知400cosθ=500-x2,
∴PB2=1000-x2
∴y=
| 9 |
| x2 |
| 4 |
| 1000-x2 |
∴y′=
| 10(x2-600)(3000-x2) |
| x3(1000-x2 )2 |
∵10
| 3 |
| 7 |
令y′=0
得x=10
| 6 |
当10
| 3 |
| 6 |
当10
| 6 |
| 7 |
∴当x=10
| 6 |
即当AP为10
| 6 |
点评:本题考查已知三角函数模型的应用问题,解答本题的关键是建立起符合条件的模型,作出正确的示意图,然后再由三角形中的相关知识进行运算,注意不同中导数的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
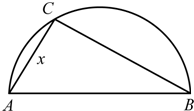 两县城A和B相距20km,现计划在两城外以AB为直径的半圆弧
两县城A和B相距20km,现计划在两城外以AB为直径的半圆弧 如图,两县城A和B相距20km,O为AB的中点,现要在以O为圆心、20km为半径的圆弧
如图,两县城A和B相距20km,O为AB的中点,现要在以O为圆心、20km为半径的圆弧 上选择一点P建造垃圾处理厂,其中MA⊥AB,NB⊥AB.已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和.统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9.记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,∠POA=θ.
上选择一点P建造垃圾处理厂,其中MA⊥AB,NB⊥AB.已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和.统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9.记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,∠POA=θ. 上选择一点P建造垃圾处理厂,其中
上选择一点P建造垃圾处理厂,其中 。已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和。统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9。记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,
。已知垃圾处理厂对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A和城B的影响度之和。统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为9。记垃圾处理厂对城A和城B的总影响度为y,设AP=xkm,

 的函数关系,并求该函数的定义域和值域;
的函数关系,并求该函数的定义域和值域; 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为 km,建在C处的垃圾处理厂对城A和城B的总影响度为
km,建在C处的垃圾处理厂对城A和城B的总影响度为 ,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.