题目内容
已知数列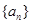 为等差数列,数列
为等差数列,数列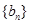 为等比数列,若
为等比数列,若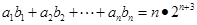 ,且
,且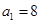 .
.
(1)求数列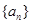 ,
,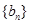 的通项公式;
的通项公式;
(2)是否存在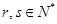 ,使得
,使得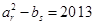 ,若存在,求出所有满足条件的
,若存在,求出所有满足条件的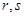 ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】
(1)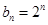 ,
,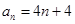 ;(2)不存在假设的
;(2)不存在假设的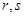 .
.
【解析】
试题分析:本题考查等差数列与等比数列的概念、通项公式等基础知识,考查思维能力、分析问题与解决问题的能力.第一问,用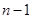 代替
代替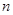 ,得到新的表达式,2个表达式相减,得到
,得到新的表达式,2个表达式相减,得到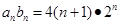 ,设
,设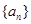 的通项公式,代入
的通项公式,代入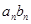 中,得到
中,得到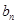 表达式,又由于
表达式,又由于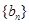 为等比数列,所以化简成关于
为等比数列,所以化简成关于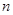 的方程,这个方程恒成立,所以
的方程,这个方程恒成立,所以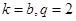 ,由于
,由于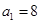 ,所以
,所以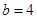 ,所以可以得到
,所以可以得到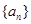
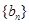 的通项公式;第二问,用反证法,找到矛盾.
的通项公式;第二问,用反证法,找到矛盾.
试题解析:(1)当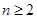 时,
时,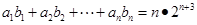
∴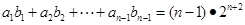 ,相减得:
,相减得:
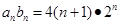 ,
,
令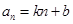
则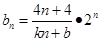 ,
,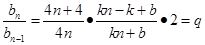 (常数),
(常数),
即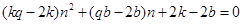 对任意
对任意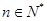 恒成立,
恒成立,
故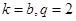 .又
.又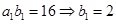 ,∴
,∴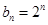 ,
,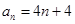 .
.
(2)假设存在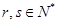 满足条件,则
满足条件,则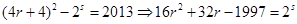 ,
,
由于等式左边为奇数,故右边也为奇数,∴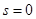 ,
,
即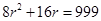 ,但左边为偶数,右边为奇数,矛盾!
,但左边为偶数,右边为奇数,矛盾!
所以不存在假设的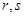 .
.
考点:1.等差、等比数列的通项公式;2.反证法.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 为等差数列,且
为等差数列,且 ,
, .
. 的通项公式;
的通项公式;  ,
, 恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由.
恒成立的实数m是否存在最小值?如果存在,求出m的最小值;如果不存在,说明理由. 为等差数列,若
为等差数列,若 且它们的前
且它们的前 项和
项和 有最大值,则使得
有最大值,则使得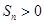 的
的 为等差数列,若
为等差数列,若 ,且它们的前
,且它们的前 项和
项和 有最大值,则使得
有最大值,则使得 的
的 为等差数列,
为等差数列,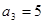 ,
, ,数列
,数列 的前
的前 项和为
项和为 ,且有
,且有
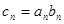 ,
, 的前
的前 ,求
,求