题目内容
若函数f(x)=l0ga(x3-ax)(a>0且a≠1)在区间(-![]() ,0)内单调递增,则a的取值范围是 ( )
,0)内单调递增,则a的取值范围是 ( )
A.[![]() ,1] B.[
,1] B.[![]() ,1] C.[
,1] C.[![]() ,+∞] D.(1,-
,+∞] D.(1,-![]() )
)
[考场错解] A当a∈(0,1)时,要使f(x)=loga(x3-ax)在区间(-![]() ,0)上单调递增.∴x3-ax>0在(-
,0)上单调递增.∴x3-ax>0在(-![]() ,0)上恒成立,∴(-
,0)上恒成立,∴(-![]() )3+
)3+![]() a≥0 a≥
a≥0 a≥![]() .综合得a∈[
.综合得a∈[![]() ,1].当a>1时,x3-ax>0在(-
,1].当a>1时,x3-ax>0在(-![]() ,0)上不可能成立.
,0)上不可能成立.
 函数,不能说 f(x)在(a,b)∪(c,d)上一定是增(减)函数. 3.设函数y=f(u),u=g(x)都是单调函数,那么复合函数y=f[g(x)]在其定义域上也是单调函数.若y=f(u)与u=g(x)的单调性相同,则复合函数y=f[g(x)]是增函数;若y=f(u),u=g(x)的单调性相反,则复合函数y=f[g(x)]是减函数.列出下表以助记忆.
函数,不能说 f(x)在(a,b)∪(c,d)上一定是增(减)函数. 3.设函数y=f(u),u=g(x)都是单调函数,那么复合函数y=f[g(x)]在其定义域上也是单调函数.若y=f(u)与u=g(x)的单调性相同,则复合函数y=f[g(x)]是增函数;若y=f(u),u=g(x)的单调性相反,则复合函数y=f[g(x)]是减函数.列出下表以助记忆.
| y=f(u) | u=g(x) | y=f[g(x)] |
| ↗ | ↗ | ↗ |
| ↗ | ↘ | ↘ |
| ↘ | ↘ | ↗ |
| ↘ | ↗ | ↘ |
上述规律可概括为“同性则增,异性则减”.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
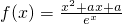 .
.