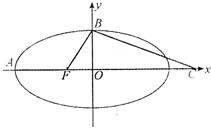
题目内容
已知椭圆C:
+
=1(a>b>0)的离心率为
,F1、F2分别为椭圆C的左、右焦点,若椭圆C的焦距为2.
(1)求椭圆C的方程;
(2)设M为椭圆上任意一点,以M为圆心,MF1为半径作圆M,当圆M与直线l:x=
有公共点时,求△MF1F2面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆C的方程;
(2)设M为椭圆上任意一点,以M为圆心,MF1为半径作圆M,当圆M与直线l:x=
| a2 |
| c |
(1)因为2c=2,且
=
,所以c=1,a=2.
所以b2=3.
所以椭圆C的方程为
+
=1.
(2)设点M的坐标为(x0,y0),
则
+
=1.
因为F1(-1,0),
=4,
所以直线l的方程为x=4.
由于圆M与l有公共点,
所以M到l的距离4-x0小于或等于圆的半径R.
因为R2=MF12=(x0+1)2+y02,
所以(4-x0)2≤(x0+1)2+y02,
即y02+10x0-15≥0.
又因为
=3(1-
),
所以3-
+10x0-15≥0.
解得
≤x0≤12.又
+
=1,∴
≤x0<2
当x0=
时,|y0|=
,
所以(S△MF1F2)max=
×2×
=
.
| c |
| a |
| 1 |
| 2 |
所以b2=3.
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设点M的坐标为(x0,y0),
则
| ||
| 4 |
| ||
| 3 |
因为F1(-1,0),
| a2 |
| c |
所以直线l的方程为x=4.
由于圆M与l有公共点,
所以M到l的距离4-x0小于或等于圆的半径R.
因为R2=MF12=(x0+1)2+y02,
所以(4-x0)2≤(x0+1)2+y02,
即y02+10x0-15≥0.
又因为
| y | 20 |
| ||
| 4 |
所以3-
3
| ||
| 4 |
解得
| 4 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| 4 |
| 3 |
当x0=
| 4 |
| 3 |
| ||
| 3 |
所以(S△MF1F2)max=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |

练习册系列答案
相关题目