题目内容
已知定义在R上的偶函数f(x)满足f(1)=0,当x>0时有 ,则不等式xf(x)>0的解集为( )
,则不等式xf(x)>0的解集为( )A.(-1,0)
B.(-1,0)∪(1,+∞)
C.(1,+∞)
D.(-∞,-1)∪(1,+∞)
【答案】分析:构造g(x)=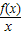 ,可得g′(x)=
,可得g′(x)=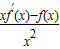 ,①当x>0时有
,①当x>0时有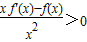 ,可得函数g(x)在x>0时单调性,可得
,可得函数g(x)在x>0时单调性,可得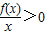 =
=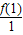 的解集,利用
的解集,利用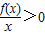 ?xf(x)>0,即可得出不等式xf(x)>0的解集;
?xf(x)>0,即可得出不等式xf(x)>0的解集;
②由于f(x)是偶函数,当x<0时,xf(x)>0?-xf(-x)<0,解得即可.
解答:解:令g(x)=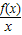 ,则g′(x)=
,则g′(x)=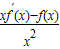 ,①当x>0时有
,①当x>0时有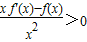 ,∴函数g(x)在x>0时单调递增,∵f(1)=0,∴
,∴函数g(x)在x>0时单调递增,∵f(1)=0,∴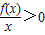 =
=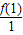 的解集为{x|x>1},又
的解集为{x|x>1},又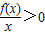 ?xf(x)>0,∴不等式xf(x)>0的解集为{x|x>1};
?xf(x)>0,∴不等式xf(x)>0的解集为{x|x>1};
②由于f(x)是偶函数,∴当x<0时,xf(x)>0?-xf(-x)<0,解得0<-x<1,即-1<x<0.
综上可知:不等式xf(x)>0的解集为(-1,0)∪(1,+∞).
故选B.
点评:通过构造函数g(x)=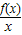 ,利用导数研究其单调性及利用偶函数的性质是解题的关键.
,利用导数研究其单调性及利用偶函数的性质是解题的关键.
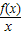 ,可得g′(x)=
,可得g′(x)=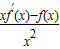 ,①当x>0时有
,①当x>0时有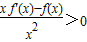 ,可得函数g(x)在x>0时单调性,可得
,可得函数g(x)在x>0时单调性,可得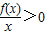 =
=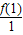 的解集,利用
的解集,利用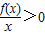 ?xf(x)>0,即可得出不等式xf(x)>0的解集;
?xf(x)>0,即可得出不等式xf(x)>0的解集;②由于f(x)是偶函数,当x<0时,xf(x)>0?-xf(-x)<0,解得即可.
解答:解:令g(x)=
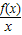 ,则g′(x)=
,则g′(x)=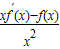 ,①当x>0时有
,①当x>0时有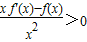 ,∴函数g(x)在x>0时单调递增,∵f(1)=0,∴
,∴函数g(x)在x>0时单调递增,∵f(1)=0,∴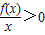 =
=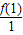 的解集为{x|x>1},又
的解集为{x|x>1},又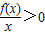 ?xf(x)>0,∴不等式xf(x)>0的解集为{x|x>1};
?xf(x)>0,∴不等式xf(x)>0的解集为{x|x>1};②由于f(x)是偶函数,∴当x<0时,xf(x)>0?-xf(-x)<0,解得0<-x<1,即-1<x<0.
综上可知:不等式xf(x)>0的解集为(-1,0)∪(1,+∞).
故选B.
点评:通过构造函数g(x)=
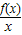 ,利用导数研究其单调性及利用偶函数的性质是解题的关键.
,利用导数研究其单调性及利用偶函数的性质是解题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目