Question

已知函数f(x)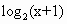＝||，实数m、n在其定义域内，且m＜n，f(m)＝f(n)．

(Ⅰ)求证：m＋n＞0；

(Ⅱ)试比较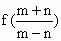与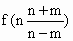的大小，并说明理由．

Answer 1

答案：
解析：

解：本小题主要考查函数的概念，不等式的知识，考查推理证明以及分析问题与解决问题的能力． 　　(Ⅰ)由f(m)＝f(n)得， 　　， 　　∴＝0 　　∴[]·[]＝0 　　∵m＜n，∴m＋1＜n＋1， 　　∴≠0 　　因此必有＝0， 　　即(m＋1)(n＋1)＝0　　∴(m＋1)(n＋1)＝1　　① 　　而0＜m＋1＜n＋1　　∴0＜m＋1＜1＜n＋1， 　　∴m＜0＜n，∴mn＜0 　　由①得mn＋m＋n＝0，∴m＋n＝－mn＞0 　　(Ⅱ) 　　由(Ⅰ)知n＞－m＞0，∴2n＞n－m＞－2m＞0， 　　∴0＜＜1，且＞1 　　∴＝ 　　又＝||＝， 　　∵＞0， 　　∴＞，∴＞． 　　解：本小题主要考查函数的概念，不等式的知识，考查推理证明以及分析问题与解决问题的能力． 　　(Ⅰ)由f(m)＝f(n)得， 　　， 　　∴＝0 　　∴[]·[]＝0 　　∵m＜n，∴m＋1＜n＋1， 　　∴≠0 　　因此必有＝0， 　　即(m＋1)(n＋1)＝0　　∴(m＋1)(n＋1)＝1　　① 　　而0＜m＋1＜n＋1　　∴0＜m＋1＜1＜n＋1， 　　∴m＜0＜n，∴mn＜0 　　由①得mn＋m＋n＝0，∴m＋n＝－mn＞0 　　(Ⅱ) 　　由(Ⅰ)知n＞－m＞0，∴2n＞n－m＞－2m＞0， 　　∴0＜＜1，且＞1 　　∴＝ 　　又＝||＝， 　　∵＞0， 　　∴＞，∴＞．