在△ABC中.角A.B.C所对的边为a.b.c.若a.b.c成等差数列.则角B的范围是0＜B≤π30＜B≤π3．题目和参考答案——青夏教育精英家教网—

题目内容

（2012•济南三模）在△ABC中，角A、B、C所对的边为a，b，c，若a，b，c成等差数列，则角B的范围是

0＜B≤

．

分析：由a，b，c成等差数列，根据等差数列的性质得到2b=a+c，解出b，然后利用余弦定理表示出cosB，把b的式子代入后，合并化简，利用基本不等式即可求出cosB的最小值，根据B的范围以及余弦函数的单调性，再利用特殊角三角函数值即可求出B的取值范围．

解答：解：由a，b，c成等差数列，得到2b=a+c，即b=

a+c

，
则cosB=

a2+c2-b2

2ac

a2+c2-(

a+c

2ac

3(a2+c2)-2ac

8ac

≥

6ac-2ac

8ac

，
因为B∈（0，π），且余弦在（0，π）上为减函数，
所以角B的范围是：0＜B≤

．
故答案为：0＜B≤

点评：此题属于解三角形的题型，涉及的知识有：等差数列的性质，余弦定理，基本不等式的运用，以及余弦函数的图象与性质，熟练掌握余弦定理及等差数列的性质是解本题的关键．

练习册系列答案

，而人均消费g（t）（元）近似地满足g（t）=120-|t-20|．
（1）求该城市的旅游日收益w（t）（万元）与时间t（1≤t≤30，t∈N^﹢）的函数关系式；
（2）求该城市旅游日收益的最小值．

（2012•济南三模）某旅游景点预计2013年1月份起前x个月的旅游人数的和p（x）（单位：万人）与x的关系近似地满足p（x）=

x（x+1）•（39-2x），（x∈N^*，且x≤12）．已知第x月的人均消费额q（x）（单位：元）与x的近似关系是q（x）=

35-2x(x∈N*，且1≤x≤6)

160

(x∈N*，且7≤x≤12)

（I）写出2013年第x月的旅游人数f（x）（单位：人）与x的函数关系式；
（II）试问2013年第几月旅游消费总额最大，最大月旅游消费总额为多少元？

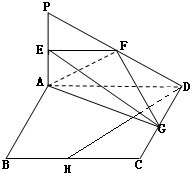（2012•济南三模）如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD，E、F、G、H分别是线段PA、PD、CD、BC的中点．
（Ⅰ）求证：BC∥平面EFG；
（Ⅱ）求证：DH⊥平面AEG；
（Ⅲ）求三棱锥E-AFG与四棱锥P-ABCD的体积比．

（2012•济南三模）已知直线l：y=x+1，圆O：x2+y2=

，直线l被圆截得的弦长与椭圆C：

=1(a＞b＞0)的短轴长相等，椭圆的离心率e=

．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点M（0，-

）的动直线l交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得无论l如何转动，以AB为直径的圆恒过定点T？若存在，求出点T的坐标；若不存在，请说明理由．

（2012•济南三模）设函数f（x）=x²-2（-1）^klnx（k∈N^*），f^′（x）表示f（x）导函数．
（I）求函数f（x）的单调递增区间；
（Ⅱ）当k为偶数时，数列{a_n}满足a₁=1，anf′(an)

n+1

-3．证明：数列{

}中不存在成等差数列的三项；
（Ⅲ）当k为奇数时，设bn=

f′(n)-n，数列{b_n}的前n项和为S_n，证明不等式(1+bn)

bn+1

＞e对一切正整数n均成立，并比较S₂₀₁₂-1与ln2012的大小．

试题分类