题目内容
如图所示:用篱笆围成一个一边靠墙的矩形菜园 ,假设墙有足够长.
(Ⅰ) 若篱笆的总长为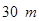 ,则这个矩形的长,宽各为多少时,菜园的面积最大?
,则这个矩形的长,宽各为多少时,菜园的面积最大?
(Ⅱ) 若菜园的面积为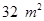 ,则这个矩形的长,宽各为多少时,篱笆的总长最短?
,则这个矩形的长,宽各为多少时,篱笆的总长最短?
(Ⅰ) 矩形的长为 ,宽为
,宽为 时,菜园的面积最大 (Ⅱ) 矩形的长为
时,菜园的面积最大 (Ⅱ) 矩形的长为 、宽为
、宽为 时,可使篱笆的总长最短
时,可使篱笆的总长最短
解析试题分析:设这个矩形的长为 ,宽为
,宽为 ,篱笆的长为
,篱笆的长为 ,面积为
,面积为 .
.
(Ⅰ) 由题知 ,由于
,由于 ,
,
∴ ,
, ,即
,即 ,当且仅当
,当且仅当 时等号成立.
时等号成立.
由
故这个矩形的长为 ,宽为
,宽为 时,菜园的面积最大.
时,菜园的面积最大.
(Ⅱ) 条件知 ,
, .
. ,当且仅当
,当且仅当 时等号成立.
时等号成立.
由
故这个矩形的长为 、宽为
、宽为 时,可使篱笆的总长最短.
时,可使篱笆的总长最短.
考点:均值不等式求最值
点评:利用均值不等式 求最值时要注意其满足的三个条件:一,
求最值时要注意其满足的三个条件:一, 都是正数,二,积为定值时和取得最值,和为定值时积为定值,三,等号成立的条件看是否满足
都是正数,二,积为定值时和取得最值,和为定值时积为定值,三,等号成立的条件看是否满足

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设x、y满足约束条件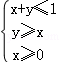 ,则z=2x﹣y的最大值为( ).
,则z=2x﹣y的最大值为( ).
| A.0 | B.2 | C.3 | D. |
实数x,y满足 ,则
,则 的最小值为3,则实数b的值为( )
的最小值为3,则实数b的值为( )
A. | B.— | C. | D.— |
 ,其中
,其中 ,求
,求 的最小值,及此时
的最小值,及此时 与
与 的值.
的值.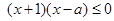 ,讨论
,讨论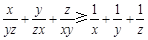 .
. 的三段式污水处理池,池高为1
的三段式污水处理池,池高为1 ,如果池的四周墙壁的建造费单价为
,如果池的四周墙壁的建造费单价为 元
元 ,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为
,池中的每道隔墙厚度不计,面积只计一面,隔墙的建造费单价为 元
元 元
元 ,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元?
,则水池的长、宽分别为多少米时,污水池的造价最低?最低造价为多少元? ,
, 及
及 的符号;
的符号; ”.
”. 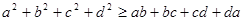
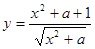 的最小值,其中
的最小值,其中