题目内容
边长为1的等边三角形ABC中,沿BC边高线AD折起,使得折后二面角B-AD-C为60°,则点A到BC的距离为
,点D到平面ABC的距离为
.
| ||
| 4 |
| ||
| 4 |
| ||
| 10 |
| ||
| 10 |
分析:根据条件确定AE为点A到直线BC的距离,DH为点D到面ABC的距离,然后利用边长关系进行求值即可.
解答: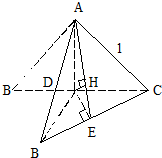 解:如图,过D点作DE⊥BC,连AE,则AE⊥BC
解:如图,过D点作DE⊥BC,连AE,则AE⊥BC
∴AE为点A到直线BC的距离
在直角三角形ADE中,AE=
=
=
.
又BC面ADE,且BC?面ABC,
∴面ABC⊥面ADE,AE为高线,作DH⊥AE于H,则DH⊥面ABC
∴DH为点D到面ABC的距离,
由DH•AE=AD•DE得DH=
=
.
故答案为:
,
.
 解:如图,过D点作DE⊥BC,连AE,则AE⊥BC
解:如图,过D点作DE⊥BC,连AE,则AE⊥BC∴AE为点A到直线BC的距离
在直角三角形ADE中,AE=
| AD2+DE2 |
(
|
| ||
| 4 |
又BC面ADE,且BC?面ABC,
∴面ABC⊥面ADE,AE为高线,作DH⊥AE于H,则DH⊥面ABC
∴DH为点D到面ABC的距离,
由DH•AE=AD•DE得DH=
| ||||||||
|
| ||
| 10 |
故答案为:
| ||
| 4 |
| ||
| 10 |
点评:本题主要考查空间点到直线和点到平面的距离,利用距离公式进行求解,考查学生的运算能力.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
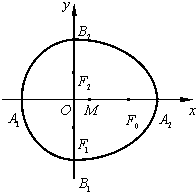 附加题:已知半椭圆
附加题:已知半椭圆 ,已知
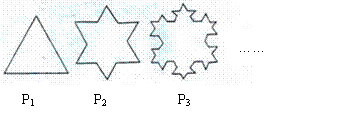
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求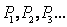 ,已知
,已知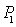 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对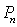 进行如下操作得到:将
进行如下操作得到:将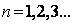 ).
).
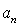 和
和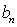 (
(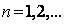 ),求
),求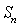 为曲线
为曲线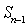 的递推关系式,并求
的递推关系式,并求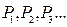 ,已知
,已知 是边长为1的等边三角形,
是边长为1的等边三角形, 是对
是对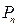 进行如下操作得到:将
进行如下操作得到:将 ).
).
 和
和 (
( ),求
),求 为曲线
为曲线 的递推关系式,并求
的递推关系式,并求