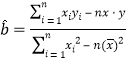题目内容
【题目】某电视台举行电视奥运知识大奖赛，比赛分初赛和决赛两部分．为了增加节目的趣味性，
初赛采用选手选一题答一题的方式进行，每位选手最多有
次选题答题的机会，选手累计答对
题或答错题即终止其初赛的比赛，答对题者直接进入决赛，答错题者则被淘汰．已知选手甲答题的正确率为
．
(1) 求选手甲可进入决赛的概率；
(2) 设选手甲在初赛中答题的个数为
，试写出的分布列，并求的数学期望．
【答案】(1) 
; (2) 见解析.
【解析】试题分析：(1)由于答对
题者直接进入决赛,故可分为三类：一类是三题全对；一类是答
题，前题错一题，第题答对；一类是答
题，前题错两题，第题答对，故可求求选手甲可进入决赛的概率；(2)依题意，
的可能取值为
，利用独立重复试验的概率公式分别求出相应的概率，从而得出的分布列，进而的数学期望.
试题解析：(1) 选手甲答道题可进入决赛的概率为
；
选手甲答道题可进入决赛的概率为
；
选手甲答5道题可进入决赛的概率为
；
∴选手甲可进入决赛的概率
+
+
．
(2) 依题意，的可能取值为
．
则有
，
，
，
因此的分布列为
|
|
|
|
|
|
|
|
．
【题目】某公司生产一种电子仪器的固定成本为20 000元，每生产一台仪器需要增加投入100元，已知总收益满足函数：R(x)＝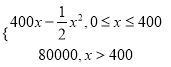
其中x是仪器的月产量．当月产量为何值时，公司所获得利润最大？最大利润是多少？
【题目】为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验.为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，结果如下表：记成绩不低于70分者为“成绩优良”.
分数 |
|
|
|
|
|
甲班频数 | 5 | 6 | 4 | 4 | 1 |
一般频数 | 1 | 3 | 6 | 5 | 5 |
（1）由以下统计数据填写下面
列联表，并判断能否在犯错误的额概率不超过0.025的前提下认为“成绩优良与教学方式有关”？
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
附：
，其中
.
临界值表
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
（2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法抽取8人进行考核.在这8人中，记成绩不优良的乙班人数为
，求的分布列及数学期望.
