Question

在直角坐标系中，设矩形OPQR的顶点按逆时针顺次为O(0,0)、P(1，t)、Q(1-2t,2+t)、R(-2t,2),其中t∈(0,+∞).

(1)求矩形OPQR在第一象限部分的面积S(t);

(2)确定函数S(t)的单调区间并加以说明.

Answer 1

解：(1)①当1-2t＞0即t∈(0,)时，点Q在第一象限(如图所示)，令矩形和y轴交于K，由QR方程为=.

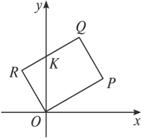
    令x=0,y=2t²+2,K(0,2t²+2),S_{四边形OPQK}=S_矩形OPQR-S_△ORK=2()²-(2t²+2)·2t

    =2(1-t+t²-t³).

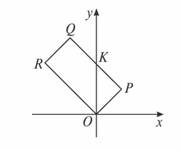
    ②当1-2t≤0,即t∈［,+∞］时，S_△ORK即为所求，点Q在y轴上或第二象限(如图所示)，由直线PQ方程为y-t=-(x-1)，令x=0,y=t+,S_△OPK=(t+)·1=(t+).

    ∴S(t)=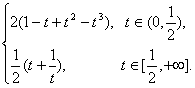

    (2)①当t∈(0,)时，S(t)=2(1-t+t²-t³),S′(t)=2(-1+2t-3t²)＜0,∴S(t)在(0,)内单调递减.

    ②当t∈(,+∞)时，S(t)=(t+),S′(t)=(1-),当1-＞0，即t∈(1,+∞)时，S(t)单调递增.当1-＜0,即t∈(,1)时，S(t)单调递减.