题目内容
(本小题满分12分)
设定义在区间 上的函数
上的函数 的图象为
的图象为 ,
, 是
是 上的任意一点,
上的任意一点, 为坐标原点,设向量
为坐标原点,设向量 =
= ,
, ,
, ,当实数λ满足x="λ" x1+(1-λ) x2时,记向量
,当实数λ满足x="λ" x1+(1-λ) x2时,记向量 =λ
=λ +(1-λ)
+(1-λ) .定义“函数
.定义“函数 在区间
在区间 上可在标准
上可在标准 下线性近似”是指 “
下线性近似”是指 “
 恒成立”,其中
恒成立”,其中 是一个确定的正数.
是一个确定的正数.
(1)求证: 三点共线;
三点共线;
(2)设函数 在区间[0,1]上可在标准
在区间[0,1]上可在标准 下线性近似,求
下线性近似,求 的取值范围;
的取值范围;
(3)求证:函数 在区间
在区间 上可在标准
上可在标准 下线性近似.
下线性近似.
(参考数据: =2.718,
=2.718, )
)
【答案】
(1)由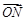 =λ
=λ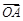 +(1-λ)
+(1-λ)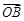 得到
得到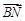 =λ
=λ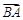 ,所以B,N,A三点共线。
,所以B,N,A三点共线。
(2)k的取值范围是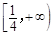 .(3)见解析。
.(3)见解析。
【解析】
试题分析:(1)由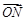 =λ
=λ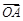 +(1-λ)
+(1-λ)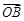 得到
得到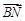 =λ
=λ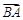 ,所以B,N,A三点共线。 ………… 2分
,所以B,N,A三点共线。 ………… 2分
(2)由x="λ" x1+(1-λ) x2与向量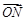 =λ
=λ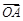 +(1-λ)
+(1-λ)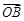 ,得N与M的横坐标相同.…4分
,得N与M的横坐标相同.…4分
对于 [0,1]上的函数y=x2,A(0,0),B(1,1), 则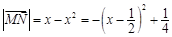 ,故
,故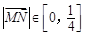 ;
;
所以k的取值范围是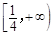 .
……………………………………………
6分
.
……………………………………………
6分
(3)对于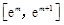 上的函数
上的函数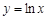 ,A(
,A(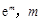 ),B(
),B(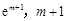 ),
),
则直线AB的方程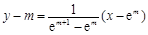 , ………………………………………………8分
, ………………………………………………8分
令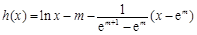 ,其中
,其中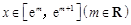 ,于是
,于是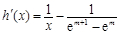 , …10分
, …10分
列表如下:
|
x |
em |
(em,em+1-em) |
em+1-em |
(em+1-em,em+1) |
em+1 |
|
|
|
+ |
0 |
- |
|
|
|
0 |
增 |
|
减 |
0 |
则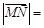
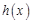 ,且在
,且在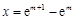 处取得最大值,
处取得最大值,
又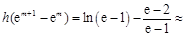 0.123
0.123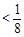 ,从而命题成立. …………………………………12分
,从而命题成立. …………………………………12分
考点:本题主要考查利用导数求闭区间上函数的最值;函数恒成立问题;向量的共线定理.
点评:本题是在新定义下考查向量共线知识以及利用导数求闭区间上函数的最值,是对知识的综合考查,属于难题.理解定义是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


