题目内容
已知实数t满足关系式![]() (a>0且a≠1)
(a>0且a≠1)
(1)令t=ax,求y=f(x)的表达式;
(2)若x∈(0,2![]() 时,y有最小值8,求a和x的值.
时,y有最小值8,求a和x的值.
答案见解析
解析:
解:(1)由loga![]() 得logat-3=logty-3logta
得logat-3=logty-3logta
由t=ax知x=logat,代入上式得x-3=![]() ,
,
∴logay=x2-3x+3,即y=a![]() (x≠0).
(x≠0).
(2)令u=x2-3x+3=(x-![]() )2+
)2+![]() (x≠0),则y=au
(x≠0),则y=au
①若0<a<1,要使y=au有最小值8,
则u=(x-![]() )2+
)2+![]() 在(0,2
在(0,2![]() 上应有最大值,但u在(0,2
上应有最大值,但u在(0,2![]() 上不存在最大值.
上不存在最大值.
②若a>1,要使y=au有最小值8,则u=(x-![]() )2+
)2+![]() ,x∈(0,2
,x∈(0,2![]() 应有最小值
应有最小值
∴当x=![]() 时,umin=
时,umin=![]() ,ymin=
,ymin=![]()
由![]() =8得a=16.∴所求a=16,x=
=8得a=16.∴所求a=16,x=![]() .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
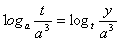 (a>0且a≠1)。
(a>0且a≠1)。