题目内容
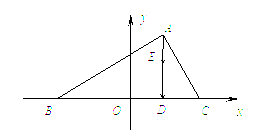 直角三角形
直角三角形![]() 的直角顶点
的直角顶点![]() 为动点,
为动点,![]() ,
,![]() 为两个定点,作
为两个定点,作![]() 于
于![]() ,动点
,动点![]() 满足
满足![]() ,当点
,当点![]() 运动时,设点
运动时,设点![]() 的轨迹为曲线
的轨迹为曲线![]() ,曲线
,曲线![]() 与
与![]() 轴正半轴的交点为
轴正半轴的交点为![]() .
.
(Ⅰ) 求曲线![]() 的方程;
的方程;
(Ⅱ) 是否存在方向向量为m![]() 的直线
的直线![]() ,与曲线
,与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 与
与![]() 的夹角为
的夹角为![]() ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
(Ⅰ)曲线![]() 的方程为
的方程为![]() ;(Ⅱ)存在满足条件的直线
;(Ⅱ)存在满足条件的直线![]() .
.
解析:
(I)由题意知,点![]() 在以
在以![]() 为直径的圆上,且除去
为直径的圆上,且除去![]() 两点.
两点.
即点![]() 坐标满足方程:
坐标满足方程:![]() .
.
设点![]() ,
,![]() ,则
,则![]() , ①
, ①
由![]() 知,
知, ,即
,即 .代入①式
.代入①式
得![]() ,即
,即![]() ,
,![]() 曲线
曲线![]() 的方程为
的方程为![]() .
.
(II)由(I)知,点![]() ,假设直线存在,可设
,假设直线存在,可设![]() ,设
,设![]() ,不妨令
,不妨令![]() ,则由
,则由 得
得 ![]() .
.
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() .
. ![]() ,
,
则

![]() ,
,
则![]() , 即
, 即![]() ,
,![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,向量
时,向量![]() 与
与![]() 的夹角为
的夹角为![]() ,不合题意舍去;
,不合题意舍去;
当![]() 时,向量
时,向量![]() 与
与![]() 的夹角为
的夹角为![]() ,符合题意.
,符合题意.
综上,存在满足条件的直线![]() .
.

练习册系列答案
相关题目
 和
和
 ,求斜边长。
,求斜边长。