题目内容
已知函数f(x)=x3+ax2+x+1在(-∞,1]上是增函数,试求a的取值范围.
解:∵f′(x)=3x2+2ax+1,
由于函数f(x)在(-∞,1]上是增函数,
∴当x∈(-∞,1]时,f′(x)≥0(在个别点f′(x)可以为0),
即3x2+2ax+1≥0在x≤1时恒成立.令g(x)=3x2+2ax+1,
∴Δ=4a2-12≤0或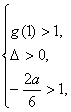
即a2≤3或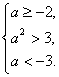
∴a2≤3,即-![]() ≤a≤
≤a≤![]() .
.

练习册系列答案
相关题目
题目内容
已知函数f(x)=x3+ax2+x+1在(-∞,1]上是增函数,试求a的取值范围.
解:∵f′(x)=3x2+2ax+1,
由于函数f(x)在(-∞,1]上是增函数,
∴当x∈(-∞,1]时,f′(x)≥0(在个别点f′(x)可以为0),
即3x2+2ax+1≥0在x≤1时恒成立.令g(x)=3x2+2ax+1,
∴Δ=4a2-12≤0或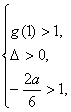
即a2≤3或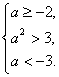
∴a2≤3,即-![]() ≤a≤
≤a≤![]() .
.
