题目内容
已知等差数列{an}的首项为正整数,公差为正偶数,且a5≥10,S15<255.
(1)求通项an;
(2)若数列a1,a3,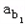 ,
,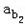 ,
,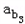 ,…
,…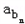 ,…,成等比数列,试找出所有的n∈N*,使
,…,成等比数列,试找出所有的n∈N*,使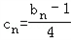 为正整数,说明你的理由.
为正整数,说明你的理由.
(1)求通项an;
(2)若数列a1,a3,
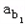 ,
,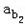 ,
,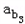 ,…
,…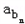 ,…,成等比数列,试找出所有的n∈N*,使
,…,成等比数列,试找出所有的n∈N*,使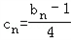 为正整数,说明你的理由.
为正整数,说明你的理由.解:(1)因为 a5≥10,S15<255,设{an}的公差为d,则有  .
.
化简可得 ,∴2d<5.
,∴2d<5.
再由{an}的首项为正整数,公差为正偶数,∴d=2,
∴a1=2
故 .
.
(2)由(1)可知a1=2,a3=6,
∴公比 ,
,
∴ ,
,
∴2·3n+1=2bn, ,
,
故 =
= .
.
此时当n=1,3,5时符合要求;当n=2,4时不符合要求.
由此可猜想:当且仅当n=2k﹣1,k∈N*时,Cn为正整数.
证明如下:
逆用等比数列的前n项和公式有: .
.
当n=2k,k∈N*时,上式括号内为奇数个奇数之和,为奇数,此时
当n=2k﹣1,k∈N*时,上式括号内为偶数个奇数之和,为偶数,此时
故满足要求的所有n为n=2k﹣1,k∈N*.
 .
.化简可得
 ,∴2d<5.
,∴2d<5.再由{an}的首项为正整数,公差为正偶数,∴d=2,
∴a1=2
故
 .
.(2)由(1)可知a1=2,a3=6,
∴公比
 ,
,∴
 ,
,∴2·3n+1=2bn,
 ,
,故
 =
= .
.此时当n=1,3,5时符合要求;当n=2,4时不符合要求.
由此可猜想:当且仅当n=2k﹣1,k∈N*时,Cn为正整数.
证明如下:
逆用等比数列的前n项和公式有:
 .
.当n=2k,k∈N*时,上式括号内为奇数个奇数之和,为奇数,此时

当n=2k﹣1,k∈N*时,上式括号内为偶数个奇数之和,为偶数,此时

故满足要求的所有n为n=2k﹣1,k∈N*.

练习册系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.