题目内容
14.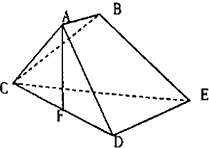 已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.
已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2,AB=1,F为CD的中点.(Ⅰ)求证:AF⊥平面CDE;
(Ⅱ)求直线AC与平面CBE所成角正弦值;
(Ⅲ)求面ACD和面BCE所成锐二面角的大小.
分析 (Ⅰ)由已知得DE⊥AF,AF⊥CD,由此能证明AF⊥平面CDE.
(2)取CE的中点Q,连结FQ,由FD,FQ,FA两两垂直,建立空间直角坐标系,利用向量法能求出直线AC与平面CBE所成角正弦值;
(Ⅲ)利用向量法能求出平面ACD和平面BCE所成锐二面角的大小.
解答 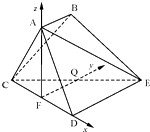 (Ⅰ)证明:∵DE⊥平面ACD,AF?平面ACD,
(Ⅰ)证明:∵DE⊥平面ACD,AF?平面ACD,
∴DE⊥AF.
又∵AC=AD,F为CD中点,∴AF⊥CD,
因CD∩DE=D,∴AF⊥平面CDE.…(4分)
(Ⅱ)解:取CE的中点Q,连接FQ,
∵F为CD的中点,∴FQ∥DE,故DE⊥平面ACD
∴FQ⊥平面ACD,又由(Ⅰ)可知FD,FQ,FA两两垂直,以O为坐标原点,
如图建立空间直角坐标系F-xyz,则F(0,0,0),C(-1,0,0),A(0,0,$\sqrt{3}$),B(0,1,$\sqrt{3}$),E(1,2,0),
∴$\overrightarrow{CB}$=(1,1,$\sqrt{3}$),$\overrightarrow{CA}$=(1,0,-$\sqrt{3}$),$\overrightarrow{CE}$=(2,2,0),
设平面CBE的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{x+y+\sqrt{3}=0}\\{2x+2y=0}\end{array}\right.$
设x=1,则$\overrightarrow{n}$=(1,-1,0)
∴cos<$\overrightarrow{CA}$,$\overrightarrow{n}$>=$\frac{\sqrt{2}}{4}$,
∴直线AC与平面CBE所成角的正弦值为$\frac{\sqrt{2}}{4}$;.…(10分)
(Ⅲ)平面ACD的一个法向量为$\overrightarrow{FQ}$=(0,1,0),则cos<$\overrightarrow{FQ}$,$\overrightarrow{n}$>=$\frac{|0-1+0|}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$
∴面ACD和面BCE所成锐二面角的大小为45°.…(13分)
点评 本题考查直线与平面垂直的证明,考查直线AC与平面CBE所成角正弦值、求面ACD和面BCE所成锐二面角的大小的求法,解题时要注意向量法的合理运用.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案| A. | (-∞,-1)(2,+∞) | B. | (2,+∞) | C. | (-∞,-1) | D. | (-1,2) |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{e}{2}$ | D. | $\frac{{\sqrt{e}}}{2}$ |
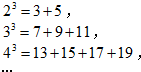 已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如:
已知大于1的任意一个自然数的三次幂都可写成连续奇数的和.如: