题目内容
已知圆C方程为:x2+y2=4.
(Ⅰ)直线l过点P(1,2),且与圆C交于A、B两点,若![]() ,求直线l的方程;
,求直线l的方程;
(Ⅱ)过圆C上一动点M作平行于x轴的直线m,设m与y轴的交点为N,若向量![]() ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
答案:
解析:
解析:
|
解(Ⅰ)①当直线 ②若直线 设圆心到此直线的距离为 ∴ 故所求直线方程为 综上所述,所求直线为 (Ⅱ)设点 则 ∵ ∴ 又∵ ∴ 轨迹是一个焦点在 |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
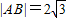 ,求直线l的方程;
,求直线l的方程;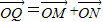 ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线. ,求直线l的方程;
,求直线l的方程; ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.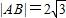 ,求直线l的方程;
,求直线l的方程; ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.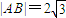 ,求直线l的方程;
,求直线l的方程;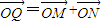 ,求动点Q的轨迹方程,并说明此轨迹是什么曲线.
,求动点Q的轨迹方程,并说明此轨迹是什么曲线.