题目内容
若f（x）=x2+ax+b-3，x∈R的图象恒过（2，0），则a2+b2的最小值为（ ）
| A．5 | B．4 | C．
| D．
|
把（2，0）代入二次函数解析式得：
4+2a+b-3=0，即2a+b=-1，解得：b=-1-2a，
则a2+b2=a2+（-1-2a）2=5a2+4a+1=5（a+
）2+
，
所以当a=-
，b=-
时，a2+b2的最小值为
．
故选D．
4+2a+b-3=0，即2a+b=-1，解得：b=-1-2a，
则a2+b2=a2+（-1-2a）2=5a2+4a+1=5（a+
| 2 |
| 5 |
| 1 |
| 5 |
所以当a=-
| 2 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
故选D．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
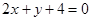与圆C：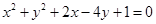
的两个交点，并且面积有最小值，求此圆的方程．
（1）求过点
的圆C的切线方程；