题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线
为抛物线![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]() 为正三角形.
为正三角形.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() ,且
,且![]() 和抛物线
和抛物线![]() 有且只有一个公共点
有且只有一个公共点![]() ,试问直线
,试问直线![]() 是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:第一问根据题意先写出抛物线的焦点坐标,设出点![]() 的坐标,利用中点坐标公式求得
的坐标,利用中点坐标公式求得![]() 的中点坐标,利用条件
的中点坐标,利用条件![]() ,结合抛物线的定义,可得
,结合抛物线的定义,可得![]() ,从而求得
,从而求得![]() 的值,进而得到抛物线的方程;第二问根据题意,结合两直线平行的条件,得到其对应的式子,根据直线过定点的条件得到结果.
的值,进而得到抛物线的方程;第二问根据题意,结合两直线平行的条件,得到其对应的式子,根据直线过定点的条件得到结果.
详解:(1)由题意知![]() ,
,
设![]() ,则
,则![]() 的中点为
的中点为![]() ,
,
因为![]() ,由抛物线的定义知:
,由抛物线的定义知:![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
由![]() ,解得
,解得![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)由(1)知![]() ,设
,设![]() ,
,![]() ,
,
因为![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,故
,故![]() ,
,
故直线![]() 的斜率为
的斜率为![]() ,
,
因为直线![]() 和直线
和直线![]() 平行,
平行,
故可设直线![]() 的方程为
的方程为![]() ,
,
代入抛物线方程得![]() ,
,
由题意知![]() ,得
,得![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,
可得直线![]() 的方程为
的方程为![]() ,
,
由![]() ,整理可得
,整理可得![]() ,
,
所以直线![]() 恒过点
恒过点![]() ,
,
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,过点
,过点![]() ,
,
所以直线![]() 恒过定点
恒过定点![]() .
.

【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
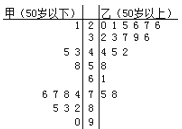
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了100名中学生进行调查.右图是根据调查的结果绘制的学生在校月消费金额的频率分布直方图.已知[350,450),[450,550),[550,650)三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群” .
(1)求m,n的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)根据已知条件完成下面2×2列联表,并判断能否有90%的把握认为“高消费群”与性别有关?
高消费群 | 非高消费群 | 合计 | |
男 | |||
女 | 10 | 50 | |
合计 |
(参考公式:![]() ,其中
,其中![]() )
)
P( | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

