题目内容
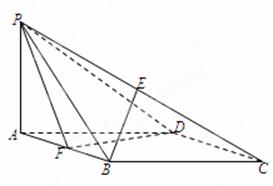
如图,在四棱锥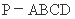 中,底面
中,底面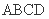 是菱形,
是菱形,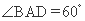 ,
,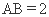 ,
,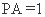 ,
,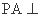 平面
平面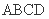 ,
, 是
是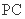 的中点,
的中点, 是
是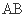 的中点.
的中点.
(Ⅰ) 求证: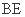 ∥平面
∥平面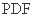 ;
;
(Ⅱ)求证:平面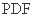 ⊥平面
⊥平面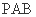 ;
;
(Ⅲ)求平面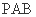 与平面
与平面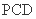 所成的锐二面角的大小.
所成的锐二面角的大小.
 |
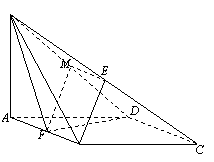 (Ⅰ) 证明:
(Ⅰ) 证明:
取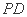 中点为
中点为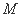 ,连
,连 . ……1分
. ……1分
∵ 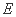 是
是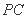 的中点
的中点
∴ 是
是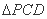 的中位线,
的中位线,
∴ 
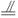
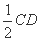 .
.
∵ 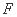 是
是 中点且
中点且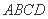 是菱形,
是菱形,
∴
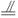
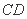 , ∴
, ∴ 
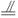
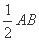 . ∴
. ∴ 
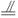
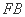
∴ 四边形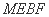 是平行四边形. 从而
是平行四边形. 从而 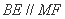 . …… 3分
. …… 3分
∵ 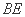
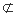 平面
平面 ,
,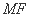
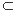 平面
平面 ,
,
∴ 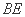 ∥平面
∥平面 ………………………………4分
………………………………4分
 ………………………………8分
………………………………8分
∵
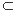 平面
平面 ∴ 平面
∴ 平面 ⊥平面
⊥平面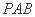 . ………………………………9分
. ………………………………9分
说明:(Ⅰ) 、(Ⅱ)也可用向量法证.

……10分
 由(Ⅱ)知
由(Ⅱ)知 ⊥平面
⊥平面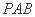 ,∴
,∴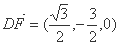 是平面
是平面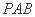 的一个法向量 …11分
的一个法向量 …11分
设平面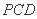 的一个法向量为
的一个法向量为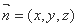
由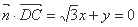 ,且由
,且由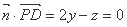
在以上二式中令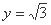 ,则得
,则得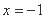 ,
,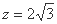 ,
,
∴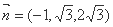 .……12分
.……12分
设平面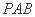 与平面
与平面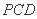 所成锐角为
所成锐角为
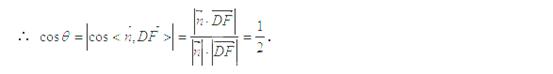
故平面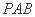 与平面
与平面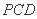 所成的锐角为
所成的锐角为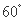 . …………………………………14分
. …………………………………14分

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
命题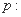
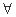
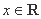 ,
,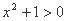 ,命题
,命题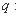
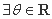 ,
,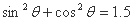 ,则下列命题中真命题是( )
,则下列命题中真命题是( )
| (A) | (B) | (C) | (D) |
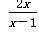 <1,q:(x-a)(x-3)>0,若綈p是綈q的必要不充分条件,则实数a的取值范围是________.
<1,q:(x-a)(x-3)>0,若綈p是綈q的必要不充分条件,则实数a的取值范围是________.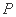 是双曲线
是双曲线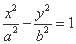 (
( ,
, )的右支上的一点,
)的右支上的一点, ,
,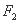 分别是左、右焦点,
分别是左、右焦点,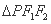 的内切圆圆心的横坐标为
的内切圆圆心的横坐标为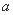 B.
B.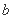 C.
C. D.
D.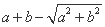
 ,若函数
,若函数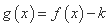 有两个不同的零点,
有两个不同的零点,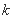 的取值范围是 .
的取值范围是 .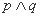
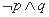
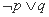
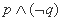
 为虚数单位)的虚部为
为虚数单位)的虚部为 C、1 D、
C、1 D、
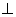 平面ADEF,
平面ADEF, 为BC的中点,M在AF上且
为BC的中点,M在AF上且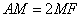 ,DP交AC与N点。
,DP交AC与N点。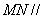 平面BCEF;
平面BCEF;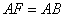 ,求DM与平面MAP所成角的正弦值。
,求DM与平面MAP所成角的正弦值。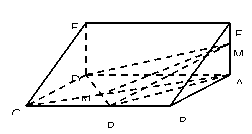
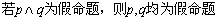 ;
;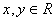 ,命题“
,命题“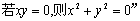 的否命题是真命题;
的否命题是真命题;