题目内容
设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
![]() .
.
(Ⅰ)求![]() ,
,![]() ,
,![]() ;
;
(Ⅱ)求证:数列![]() 是等比数列;
是等比数列;
(Ⅲ)求数列![]() 的前
的前![]() 项和
项和![]() .
.
解:(I)由题意,当![]() 时,得
时,得![]() ,解得
,解得![]() .
.
当![]() 时,得
时,得![]() ,解得
,解得![]() .
.
当![]() 时,得
时,得![]() ,解得
,解得![]() .
.
所以![]() ,
,![]() ,
,![]() 为所求. ……………3分
为所求. ……………3分
(Ⅱ) 因为![]() ,所以有
,所以有![]() 成立.
成立.
两式相减得:![]() .
.
所以![]()
![]() ,即
,即![]() . …………5分
. …………5分
所以数列![]() 是以
是以![]() 为首项,公比为
为首项,公比为![]() 的等比数列.……………7分
的等比数列.……………7分
(Ⅲ)由(Ⅱ) 得:![]() ,即
,即![]()
![]() .
.
则![]()
![]() . ……………8分
. ……………8分
设数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
则![]() ,
,
所以![]() ,
,
所以![]() ,
,
即![]()
![]() . ……………11分
. ……………11分
所以数列![]() 的前
的前![]() 项和
项和![]() =
=![]() ,
,
整理得,![]()
![]() . ……………13分
. ……………13分

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 .
. ,数列
,数列 的前
的前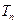 ,求证:
,求证: .
. 的前
的前 项和为
项和为 ,且满足
,且满足 .
. 与
与 两项之间插入
两项之间插入 个数构成等差数列,其公差为
个数构成等差数列,其公差为 ,求数列
,求数列 的前
的前 .
. 的前
的前 项和为
项和为 ,且满足
,且满足
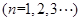 .
. 为等比数列;
为等比数列; ;
; 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列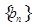 的前
的前 .
. 
 的前
的前 项和为
项和为 ,且
,且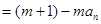 对于
对于 为常数,且
为常数,且
 ,数列
,数列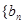

 ,
,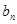
 )(
)( ,
, ,求证:数列
,求证:数列

