题目内容
在△ABC中，角A，B，C的对边分别是a，b，c，且b2=ac=a2-c2+bc，
（1）求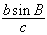
的值；
（2）试判断△ABC的形状，并说明理由。
（1）求
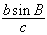的值； （2）试判断△ABC的形状，并说明理由。
解：（1）由
，
在△ABC中，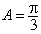
，
由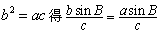
，
由正弦定理得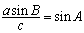
，
所以，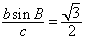
；
（2）△ABC为等边三角形，下证之：
由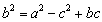
知
不失一般性，可设c=1，
则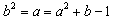
，
消去a得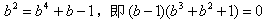
，
所以b=1，a=1，即证。
，在△ABC中，
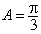，由
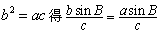，由正弦定理得
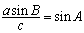， 所以，
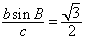；（2）△ABC为等边三角形，下证之：
由
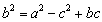知不失一般性，可设c=1，
则
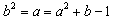，消去a得
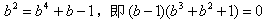，所以b=1，a=1，即证。
练习册系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |