题目内容
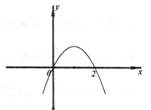
已知定义在R上的函数f(x)，其导函数f′(x)的大致图像如图所示，则下列叙述正确的是( )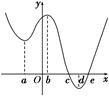 
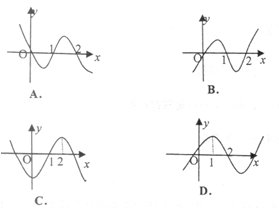
| A．f(b)>f(c)>f(d) | B．f(b)>f(a)>f(e) |
| C．f(c)>f(b)>f(a) | D．f(c)>f(e)>f(d) |
C
解析试题分析：由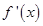
图象可知函数在
上单调递增，在
上单调递减速，
上单调递增，可知
在递增区间且有
故f(c)>f(b)>f(a)．
考点：导数与函数的单调性．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若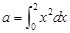
,
,
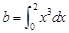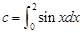,则
的大小关系是( )．
A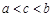． | B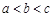． | C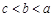． | D． |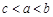
设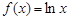
，若
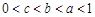，则
，
，
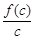的大小关系为（ ）
A． |
B． |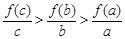
C． |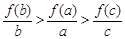
D． |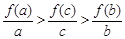
函数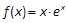
,则
（ ）．
A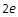． | B． | C． | D． |
一物体的运动方程为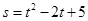
，其中s的单位是米，t的单位是秒，那么物体在4秒末的瞬时速度是（ ）
| A．8米/秒 | B．7米/秒 | C．6米/秒 | D．5米/秒 |
已知函数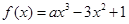
，若
存在唯一的零点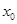
，且
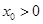，则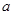
的取值范围是
A． | B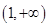． | C． | D． |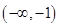
设定义在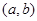
上的可导函数
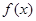的导函数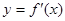
的图象如右所示,则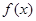的极值点的个数为 （ ）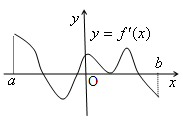
| A．1 | B．2 | C．3 | D．4 |
的导函数
的图像如图所示，则
设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(1－x)f′(x)的图象如图所示，则下列结论中一定成立的是( )
| A．函数f(x)有极大值f(2)和极小值f(1) |
| B．函数f(x)有极大值f(－2)和极小值f(1) |
| C．函数f(x)有极大值f(2)和极小值f(－2) |
| D．函数f(x)有极大值f(－2)和极小值f(2) |