题目内容
实验表明,某型号的汽车每小时的耗油量y(升)与速度x(千米/小时)的关系式为y=3(
-
+2),已知甲乙两地相距180千米,最高时速为V千米/小时.
(1)当车速度x(千米/小时)时,从甲地到乙地的耗油量为f(x)(升),求函数f(x)的解析式并指出函数的定义域;
(2)当车速为多大时,从甲地到乙地的耗油量最少?
| x3 |
| 903 |
| x |
| 80 |
(1)当车速度x(千米/小时)时,从甲地到乙地的耗油量为f(x)(升),求函数f(x)的解析式并指出函数的定义域;
(2)当车速为多大时,从甲地到乙地的耗油量最少?
(1)∵每小时的耗油量y(升)与速度x(千米/小时)的关系式为y=3(
-
+2),
甲乙两地相距180千米,当车速度x(千米/小时)时,
f(x)=
×y=540(
-
+
),x∈(0,V]…6分(2)∵f(x)=540(
-
+
),
∴f′(x)=540(
-
)
令f′(x)=0,解得x=90…8分
若V<90,有f′(x)<0,则函数f(x)在区间(0,V)内为单调减函数,所以车速为V(千米/小时)时,从甲地到乙地的耗油量最小;…11分
若V≥90,当0<x<90时,f′(x)<0;当90<x≤V时,f′(x)>0,所以,当x=90时,f(x)最小.…14分
综上:若V<90,车速为V(千米/小时)时,从甲地到乙地的耗油量最小;若V≥90,车速为90(千米/小时)时,从甲地到乙地的耗油量最小.…15
| x3 |
| 903 |
| x |
| 80 |
甲乙两地相距180千米,当车速度x(千米/小时)时,
f(x)=
| 180 |
| x |
| x2 |
| 903 |
| 1 |
| 80 |
| 2 |
| x |
| x2 |
| 903 |
| 1 |
| 80 |
| 2 |
| x |
∴f′(x)=540(
| 2x |
| 903 |
| 2 |
| x2 |
令f′(x)=0,解得x=90…8分
若V<90,有f′(x)<0,则函数f(x)在区间(0,V)内为单调减函数,所以车速为V(千米/小时)时,从甲地到乙地的耗油量最小;…11分
若V≥90,当0<x<90时,f′(x)<0;当90<x≤V时,f′(x)>0,所以,当x=90时,f(x)最小.…14分
综上:若V<90,车速为V(千米/小时)时,从甲地到乙地的耗油量最小;若V≥90,车速为90(千米/小时)时,从甲地到乙地的耗油量最小.…15

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
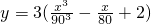 ,已知甲乙两地相距180千米,最高时速为V千米/小时.
,已知甲乙两地相距180千米,最高时速为V千米/小时.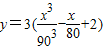 ,已知甲乙两地相距180千米,最高时速为V千米/小时.
,已知甲乙两地相距180千米,最高时速为V千米/小时. (升)与速度
(升)与速度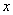 (千米/小时)的关系式为
(千米/小时)的关系式为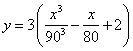 ,已知甲乙两地相距180千米,最高时速为
,已知甲乙两地相距180千米,最高时速为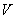 千米/小时。
千米/小时。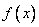 (升),求函数
(升),求函数