题目内容
 设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},
设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},
P={x|5-2a<x<3a},则实数a的取值范围是
- A.-5<a<2
- B.1<a<2
- C.1<a≤2
- D.-5≤a≤2
C
分析:非空集合S、P,S∩P=∅,考查两个集合的区间端点之间的大小关系.
解答:由题图可知,S∩P=∅,S≠∅,P≠∅,而
∴1<a≤2.
故选C.
点评:本题考查一元二次不等式的解法,以及用图示法表示2个集合间的关系和运算.
分析:非空集合S、P,S∩P=∅,考查两个集合的区间端点之间的大小关系.
解答:由题图可知,S∩P=∅,S≠∅,P≠∅,而

∴1<a≤2.
故选C.
点评:本题考查一元二次不等式的解法,以及用图示法表示2个集合间的关系和运算.

练习册系列答案
相关题目
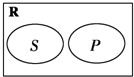 设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},
设全集为实数集R,已知非空集合S,P相互关系如图所示,其中S={x|x>10-a2},P={x|5-2a<x<3a},则实数a的取值范围是( )
| A、-5<a<2 | B、1<a<2 | C、1<a≤2 | D、-5≤a≤2 |

