Question

如图，树顶A距地面7.7米，树上另一点距地面4.7米，人眼C离地面1.7米．问人离此树多远时，看树冠AB这一段的视角最大？

Answer 1

分析：过点C作CD⊥AB，设CD=x，根据已知中树顶A距地面7.7米，树上另一点B距地面4.7米，人眼C离地面1.7米．我们易求出tan∠ACB，即tan（∠ACD-∠BCD）的表达式，进而根据基本不等式，求出tan∠ACB的范围及tan∠ACB取最大值时x的值，进而得到答案．

解答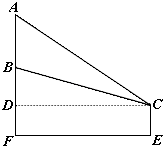：解；如图，过点C作CD⊥AB，
则AD=6，BD=3，设CD=x．
由图可知：tan∠ACB=tan（∠ACD-∠BCD）
=

tan∠ACD-tan∠BCD

1+tan∠ACD•tan∠BCD

．
=

6 x - 3 x

1+ 6 x • 3 x

=

3

x+ 18 x

≤

3

2 18

=

2

4

．
故当x=

18

x

，即x=3

2

时，视角最大．

点评：本题考查的知识点是三角函数的实际应用，两角差的正切公式，及基本不等式，其中构造适当的三角形，将问题转化为一个三角函数问题是解答本题的关键．