题目内容

在斜三棱柱ABC-A1B1C1中，A0，B0，分别为侧棱AA1，BB1上的点，且知BB0：B0B1=3：2，过A0，B0，C1的截面将三棱柱分成上下两个部分体积之比为2：1，则AA0：A0A1=（　　）
A．2：3B．4：3C．3：2D．1：1
精英家教网
上下二部分体积高相等，体积之比为为两个四边形面积之比，
设二梯形高为h1，
V上
V下
=
S四边形ABBOAO
S四边形BOB1A1AO
=
(AAO+BBO)h1 
2
，
AAO+BBO=AOA1+BOB1，设侧棱长为a，
AAO
AA1
=k，AA1=a，AAO=ak，AOA1=a（1-k），
BBO=
3a
5
，BOB1=
2a
5
，
a
5
=a（1-k）-ak，k=
2
5
，
AAO
AA1
=
2
5
，
AAO
AOA1
=
2
3
．
故选A．
练习册系列答案
相关题目
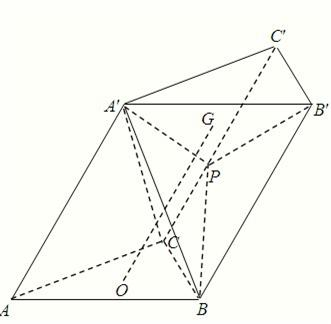精英家教网在斜三棱柱ABC-A′B′C′中，底面△ABC为正三角形，设AA′：AC=λ．顶点A′在底面ABC上的射影O是△ABC的中心，P为侧棱CC′中点，G为△PA′B′的重心．
（Ⅰ）求证：OG∥平面AA′B′B；
（Ⅱ）当λ=
2
时，求证：平面A′B′P⊥平面BB′C′C；
（Ⅲ）当λ=1时，求二面角C-A′B-P的大小．
（2008•武汉模拟）如图，在斜三棱柱ABC-A'B'C'中，∠ABC=90°，则侧面A'ACC'⊥侧面ABC，又AA'和底面所成60°的角，且AA'=2a，AB=BC=
2
a．
（1）求平面ABB'A'与底面ABC所成的角的正切值；
（2）求侧面BB'C'C的面积．
在斜三棱柱ABC-A′B′C′中，底面△ABC为正三角形，设AA′：AC=λ．顶点A′在底面ABC上的射影O是△ABC的中心，P为侧棱CC′中点，G为△PA′B′的重心．
（Ⅰ）求证：OG∥平面AA′B′B；
（Ⅱ）当λ=时，求证：平面A′B′P⊥平面BB′C′C；
（Ⅲ）当λ=1时，求二面角C-A′B-P的大小．
在斜三棱柱ABC-A′B′C′中，底面△ABC为正三角形，设AA′：AC=λ．顶点A′在底面ABC上的射影O是△ABC的中心，P为侧棱CC′中点，G为△PA′B′的重心．
（Ⅰ）求证：OG∥平面AA′B′B；
（Ⅱ）当λ=时，求证：平面A′B′P⊥平面BB′C′C；
（Ⅲ）当λ=1时，求二面角C-A′B-P的大小．
如图，在斜三棱柱ABC-A'B'C'中，∠ABC=90°，则侧面A'ACC'⊥侧面ABC，又AA'和底面所成60°的角，且AA'=2a，AB=BC=．
（1）求平面ABB'A'与底面ABC所成的角的正切值；
（2）求侧面BB'C'C的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网