题目内容
已知函数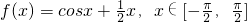 ,
,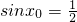 ,
,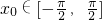 .那么下面命题中真命题的序号是
.那么下面命题中真命题的序号是
①f(x)的最大值为f(x0)
②f(x)的最小值为f(x0)
③f(x)在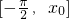 上是增函数
上是增函数
④f(x)在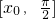 上是增函数.
上是增函数.
- A.①③
- B.①④
- C.②③
- D.②④
A
分析:由于 ,则可求出x0,再利用导函数即可求出原函数的最值及其在
,则可求出x0,再利用导函数即可求出原函数的最值及其在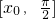 和
和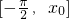 上的单调性.
上的单调性.
解答:因为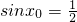 ,
,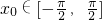 ,所以
,所以 .
.
函数的导数为 ,
,
由 ,解得
,解得 ,
,
又因为 ,所以
,所以 ,此时函数单调递增,
,此时函数单调递增,
由 ,解得
,解得 ,
,
又因为 ,所以
,所以 ,此时函数单调递减,所以①③正确,
,此时函数单调递减,所以①③正确,
故答案选A.
点评:本题考查的知识点是,判断命题真假,同时考查了导数在研究函数单调性中的应用,我们要对四个结论逐一进行判断,可以得到正确的结论.注意导数在研究函数单调性中的应用为高考必考知识点.
分析:由于
 ,则可求出x0,再利用导函数即可求出原函数的最值及其在
,则可求出x0,再利用导函数即可求出原函数的最值及其在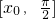 和
和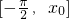 上的单调性.
上的单调性.解答:因为
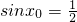 ,
,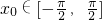 ,所以
,所以 .
.函数的导数为
 ,
,由
 ,解得
,解得 ,
,又因为
 ,所以
,所以 ,此时函数单调递增,
,此时函数单调递增,由
 ,解得
,解得 ,
,又因为
 ,所以
,所以 ,此时函数单调递减,所以①③正确,
,此时函数单调递减,所以①③正确,故答案选A.
点评:本题考查的知识点是,判断命题真假,同时考查了导数在研究函数单调性中的应用,我们要对四个结论逐一进行判断,可以得到正确的结论.注意导数在研究函数单调性中的应用为高考必考知识点.

练习册系列答案
相关题目
 ,用二分法求方程
,用二分法求方程 内近似解的过程中,取区间中点
内近似解的过程中,取区间中点 ,那么下一个有根区间为 ( )
,那么下一个有根区间为 ( )